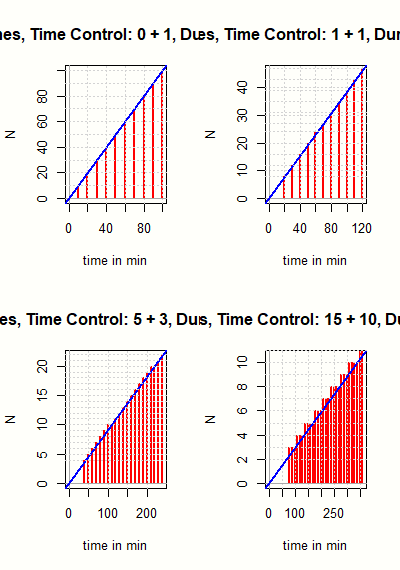
Es wird ein Turniermodus vorgeschlagen und beschrieben, der die meisten Vorteile der bisherigen Arena-Turniere auf Lichess besitzt. Die Anzahl der Partien pro Turnier ist beschränkt und die möglichen Zeitkontrollen ergeben sich aus der Fibonacci-Folge. Die bisherigen Arena-Turniere bevorzugen Spieler, die schneller spielen als nach der eigentlich vorgesehenen Zeitkontrolle. Die Fibonacci-Arena soll dagegen einen Anreiz liefern, die Bedenkzeit voll auszunutzen und wird daher einen anderen Spielerkreis ansprechen. Diskutiert werden die Vor- und Nachteile der Turniertypen und es werden Hinweise zur Durchführung der Fibonacci-Arena gegeben.
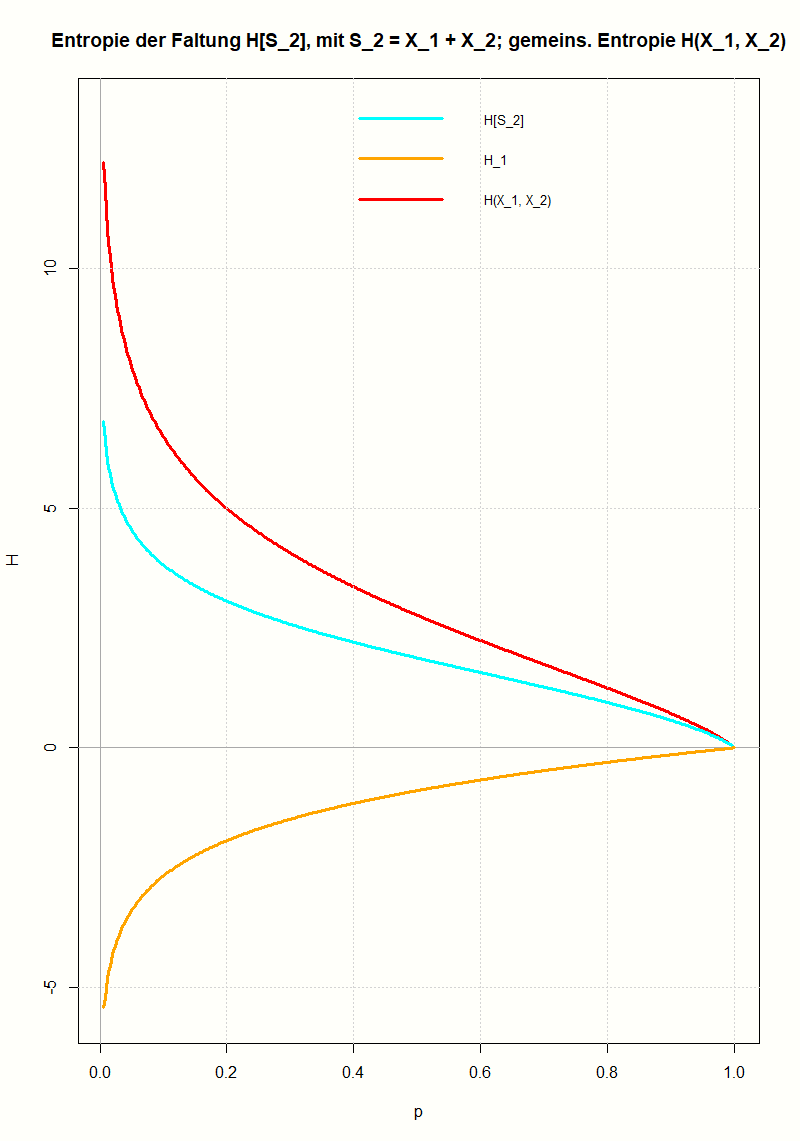
Am Beispiel der geometrischen Verteilung wird gezeigt, wie man die Entropie einer Faltung berechnet und wie sie mit den Entropien der Ausgangsverteilungen zusammenhängt. Mit Hilfe der Log-Summen-Ungleichung (einer Folgerung aus der Jensenschen Ungleichung) lässt sich das Ergebnis für beliebige Verteilungen verallgemeinern.
An einfachen Beispielen wird gezeigt, welche Eigenschaften verwendet werden, um eine Markov-Kette zu definieren. Sie stellt eine Verallgemeinerung der unabhängigen Zufallsvariablen dar. Und zwar in dem Sinn, dass in einer Folge von Zufallsvariablen jede Zufallsvariable nur vom Wert der vorhergehenden, nicht aber von noch weiter zurückliegenden Zufallsvariablen abhängt. Die zentrale mathematische Größe zur Beschreibung einer Markov-Kette ist die Übergangsmatrix, welche die Übergangswahrscheinlichkeiten zwischen den möglichen Zuständen (Werten der Zufallsvariablen) festlegt.
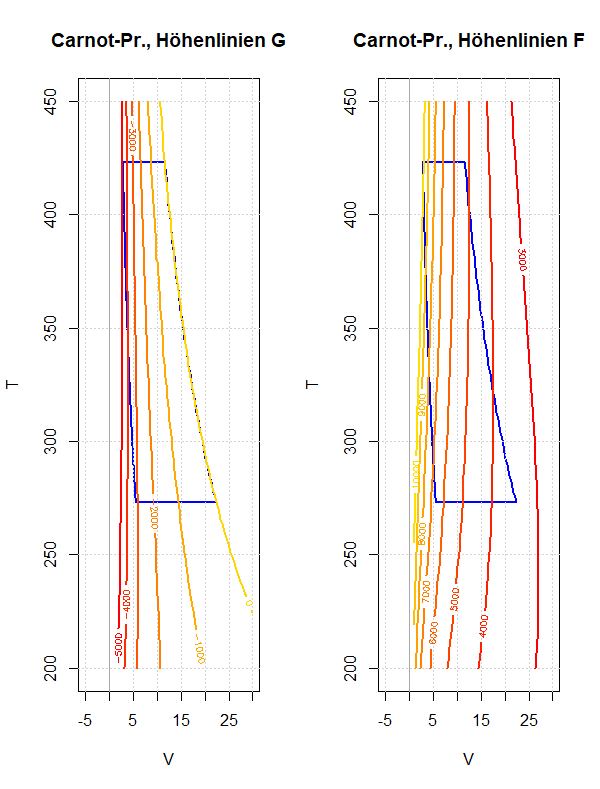
Am Beispiel des Carnot-Prozesses soll das Verhalten der freien und der gebundenen Energie während eines Umlaufs diskutiert werden. Dies soll die Bedeutung dieser thermodynamischen Potentiale besser verständlich machen; speziell ob und wie sie als Arbeitsfähigkeit beziehungsweise Wärmeinhalt eines Systems interpretiert werden können.
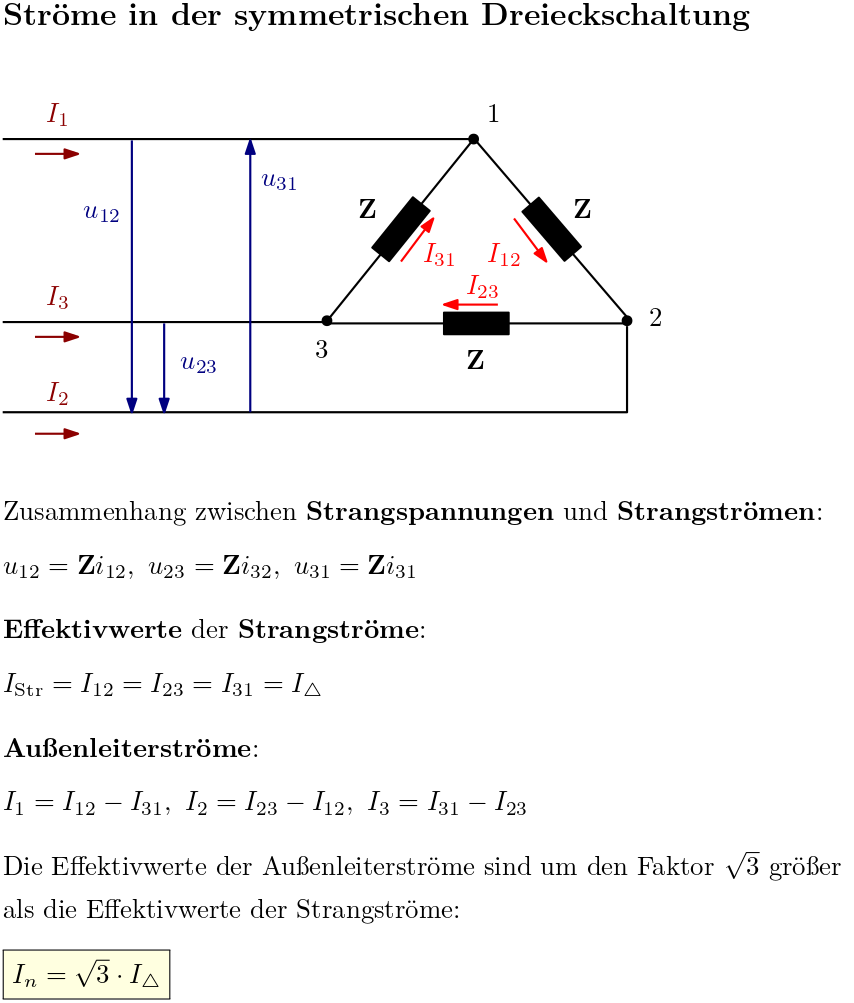
Werden die Verbraucher eines Mehrphasensystems zu einem Ring verkettet, so spricht man im Fall des Dreiphasensystems von der Dreieckschaltung. Diskutiert werden der Aufbau der symmetrischen Dreieckschaltung, die Zusammenhänge zwischen Außenleiterspannung und Strangspannung beziehungsweise Außenleiterstrom und Strangstrom sowie die Berechnung der Leistungen (Wirkleistung, Blindleistung, Scheinleistung).
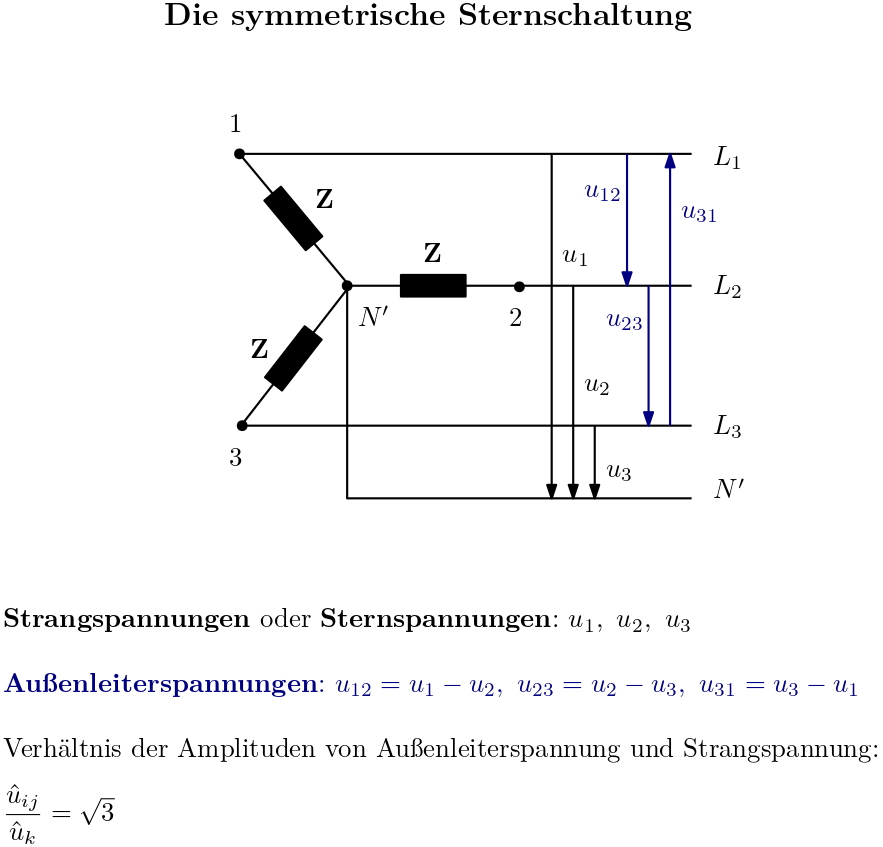
Ein Generator mit gegeneinander verdrehten Wicklungen erzeugt phasenverschobene Spannungen. Diese Spannungen können auf verschiedene Arten eingesetzt werden, um Verbraucher zu versorgen. Eine Möglichkeit besteht darin, sowohl die Spannungsquellen als auch die Verbraucher zu verketten und sie in je einem Sternpunkt zusammenzuführen; die beiden Sternpunkte werden dann leitend miteinander verbunden. Es entsteht die Sternschaltung, die in der Technik mit drei Phasen eingesetzt wird. Die symmetrische Sternschaltung wird entwickelt und die relevanten Leistungen werden berechnet.
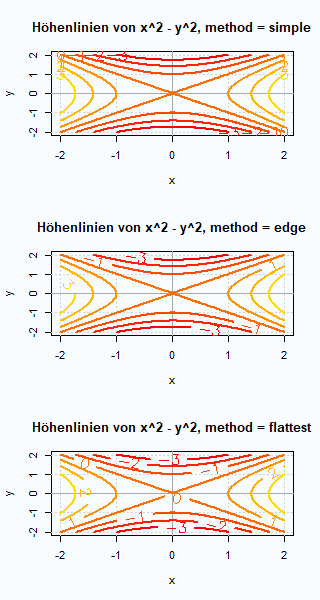
Die Funktion contour() ermöglicht es die Höhenlinien einer reellwertigen Funktion darzustellen, die auf einem zweidimensionalen Gebiet definiert ist. Die Höhenlinien geben manchmal den Graphen besser wieder als eine perspektivische dreidimensionale Darstellung wie sie etwa mit persp() erzeugt werden kann. An einfachen Beispielen werden die Eingabewerte von contour() erläutert.
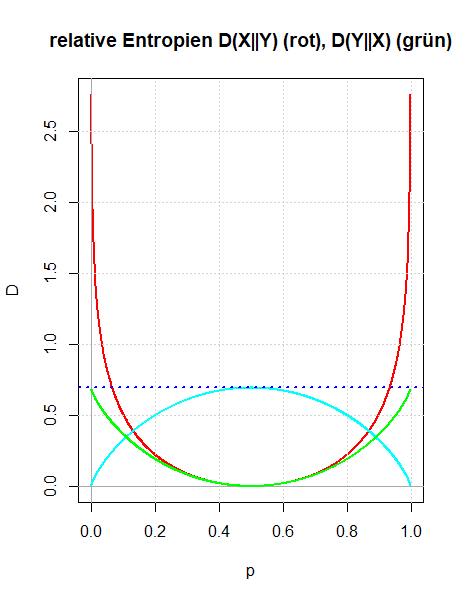
Es werden zwei Zugänge gezeigt, wie man die relative Entropie motivieren kann: Entweder als Verallgemeinerung der gegenseitigen Information oder indem man die Überlegungen Boltzmanns zur Definition der Entropie in dem Sinn verallgemeinert, dass man die Voraussetzung der Gleichwahrscheinlichkeit der Mikrozustände aufgibt. Die Bedeutung der relativen Entropie als einer Größe, die quantifiziert, wie unterschiedlich zwei Wahrscheinlichkeitsverteilungen sind, wird durch den zweiten Zugang besser verständlich.
Ludwig Boltzmann gab eine mikroskopische Erklärung für die thermodynamische Entropie, die nach dem zweiten Hauptsatz der Thermodynamik niemals abnehmen kann. Diese Überlegungen werden verwendet, um zu motivieren, wie die Entropie der Wahrscheinlichkeitstheorie definiert wird, die die Ungewissheit über den Wert einer Zufallsvariable quantifizieren soll.
Die Entropie einer Zufallsvariable, die gemeinsame Entropie zweier Zufallsvariablen und die gegenseitige Information werden am Beispiel der Wartezeitprobleme beim Ziehen ohne Zurücklegen veranschaulicht. Dazu werden als Zufallsvariablen die Wartezeit bis zum ersten Treffer und die Wartezeit vom ersten bis zum zweiten Treffer verwendet.
Überträgt man den Begriff der Entropie einer Zufallsvariable auf die Wahrscheinlichkeitsverteilungen von zwei Zufallsvariablen, so ist es naheliegend die gemeinsame Entropie und die bedingte Entropie einzuführen, die über die Kettenregel miteinander verknüpft sind. Diese wiederum motiviert die Einführung einer neuen Größe, der gegenseitigen Information zweier Zufallsvariablen. Sie ist symmetrisch in den beiden Zufallsvariablen und beschreibt die Information, die in einer Zufallsvariable über die andere Zufallsvariable enthalten ist. An einfachen Beispielen wird die Definition der gegenseitigen Information motiviert und veranschaulicht.
Die Entropie wurde eingeführt als ein Maß für die Ungewissheit über den Ausgang eines Zufallsexperimentes. Entsprechend kann man eine bedingte Entropie definieren, wenn man die bedingten Wahrscheinlichkeiten verwendet, wobei man als Bedingung entweder ein Ereignis oder eine Zufallsvariable zulässt. Die Definition der bedingten Entropie und ihr Zusammenhang mit der gemeinsamen Entropie zweier Zufallsvariablen (Kettenregel) wird an einfachen Beispielen erläutert.
Akzeptiert man die Entropie als eine Kenngröße einer Wahrscheinlichkeitsverteilung, die die Ungewissheit über den Ausgang eines Zufallsexperimentes beschreibt, so wird man fordern, dass sich bei unabhängigen Zufallsexperimenten die Entropien addieren.
Um diese Aussage schärfer formulieren zu können, wird die gemeinsame Entropie H(X, Y) von zwei Zufallsvariablen eingeführt.
Es wird gezeigt, dass die übliche Definition der Entropie die Additivitätseigenschaft bei unabhängigen Zufallsvariablen X und Y besitzt.
Am Beispiel der isochoren Erwärmung werden die Eigenschaften der freien Energie F = U - TS und der gebundenen Energie G = TS erläutert. Speziell wird gezeigt, wie man ihre Veränderung darstellen kann, wenn man vom US-Diagramm zum TS-Diagramm übergeht.
Die Funktionen substr() und substring() werden eingesetzt, um aus einem String einen Substring zu extrahieren. Dazu müssen die Indizes angegeben werden, wo sich der Substring befindet. In der replacement-Version kann der Substring verändert werden, der Rest des Strings bleibt unverändert. Da die Funktionen vektorisiert sind, kann anstelle einer einzigen Zeichenkette auch ein Vektor von Zeichenketten verarbeitet werden.
Die Funktion paste() dient ähnlich wie die Funktion paste0() dazu, mehrere Vektoren in Zeichenketten zu verwandeln, die entsprechenden Komponenten zusammenzufügen (1.Schritt) und diese zu einer einzigen Zeichenkette zusammenzusetzen (2. Schritt). In beiden Schritten kann eine Zeichenkette als Trennungszeichen eingefügt werden (die Argumente sep beziehungsweise collapse). Die Funktion paste0() besitzt kein Argument sep; für Aufgaben, die sich auch mit paste0() erledigen lassen, können dadurch mit paste() einfachere Quelltexte geschrieben werden. Beispiele und Spezialfälle werden erläutert.
Die Funktion paste0() verknüpft entsprechende Komponenten von mehreren Vektoren; die Komponenten werden dazu in Zeichenketten verwandelt. Wird das Argument collapse nicht gesetzt, wird dieser Vektor von Zeichenketten zurückgegeben. Wird das Argument collapse gesetzt (es muss eine Zeichenkette sein), werden die Komponenten zu einer einzigen Zeichenkette zusammengefügt, wobei das Argument collapse als Trennungszeichen eingefügt wird. Typische Anwendungen und Spezialfälle werden erläutert.
Die Funktion format.info() liefert Informationen über den Rückgabewert von format(). Die Funktion formatC() bildet eine Alternative zu format() und mit ihr werden Formatierungsanweisungen ähnlich wie in der Programmiersprache C formuliert. Die Funktion prettyNum() wird von formatC() intern genutzt, um Zahlen zu formatieren.
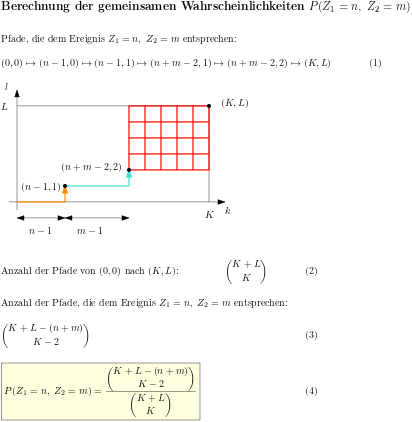
Die Zufallsexperimente Ziehen mit Zurücklegen beziehungsweise Ziehen ohne Zurücklegen werden umformuliert in eine Zufallsbewegung auf einem Gitter. Dadurch lassen sich viele Herleitungen besser veranschaulichen. Gezeigt wird dies hier für die Verteilungen der Zufallsvariablen, die die Anzahl der Treffer oder die Wartezeit bis zu einem bestimmten Treffer beschreiben.
Um zu quantifizieren, wie gut ein Taylor-Polynom eine gegebene Funktion f(x) approximiert, wird das Restglied in Integraldarstellung hergeleitet. Ist f(x) genügend oft stetig differenzierbar, wird es sukzessive durch partielle Integration berechnet.
An zwei einfachen Beispielen (Logarithmusfunktion und Wurzelfunktion) wird demonstriert, wie man zu einer gegeben Funktion f(x) das Taylor-Polynom berechnet:
Dazu wird der Ansatz verallgemeinert, wie zum Entwicklungspunkt 0 aus den Ableitungen von f(x) die Koeffizienten des Taylor-Polynoms berechnet werden.
An zwei einfachen Beispielen (Exponentialfunktion und Kosinusfunktion) wird die Vorgehensweise demonstriert, wie man zu einer gegeben Funktion das Taylor-Polynom berechnet: Am Entwicklungspunkt wird der Funktionswert und der Wert der Ableitungen (bis zum Grad n) berechnet. Das Taylor-Polynom ist das Polynom n-ten Grades, das genau diese Funktions- und Ableitungswerte im Entwicklungspunkt besitzt. Weitere Eigenschaften der Taylor-Entwicklung werden nur angedeutet, aber hier nicht diskutiert.
Die Funktion format() dient dazu Ausgaben zu formatieren. Meist wird sie verwendet, um Gleitkommazahlen mit einer geeigneten Anzahl von gültigen Stellen darzustellen. Diese und weitere Einsatzmöglichkeiten (wissenschaftliche Darstellung von Zahlen) sowie Eigenschaften der Implementierung von format() (wie etwa weitere Eingabewerte, der Rückgabewert von format()) werden an zahlreichen Beispielen erläutert.
Die Funktion cat() bietet die einfachste Möglichkeit, Informationen über ein Objekt oder mehrere Objekte auf der Konsole auszugeben. Die Besonderheiten der Funktion werden vorgestellt, wie etwa spezielle Formatierungsanweisungen oder die Möglichkeit die Ausgabe in eine Datei umzuleiten.
Es werden die Wartezeitprobleme bei den beiden Zufallsexperimenten Ziehen mit Zurücklegen beziehungsweise Ziehen ohne Zurücklegen untersucht.
Bei diesen Zufallsexperimenten befinden sich in einer Urne Treffer und Nieten. Mit Wartezeitproblem ist gemeint, dass man eine Zufallsvariable definiert, die angibt nach wie vielen Zügen der r-te Treffer aus der Urne entnommen wird. Zur Vorbereitung werden die Zusammenhänge zwischen Binomialverteilung, geometrischer Verteilung und hyper-geometrischer Verteilung gezeigt.
Die geometrische Verteilung kann als Verteilung von Wartezeiten aufgefasst werden, wenn man einen Münzwurf solange wiederholt bis der erste Treffer eintritt: man berechnet die Wahrscheinlichkeiten der Anzahl der nötigen Würfe. Man kann dieses Wartezeitproblem verallgemeinern, indem man nicht bis zum ersten sondern bis zum r-ten Treffer wartet. Die Verteilung dieser Wartezeiten wird berechnet und die Eigenschaften der dabei entstehenden Verteilung wird untersucht.
Das asymptotische Verhalten der Fakultät n! wird in sehr guter Näherung durch die Stirling-Approximation beschrieben. Sie wird hier durch die sogenannte Laplace-Methode hergeleitet. Dabei wird die Fakultät mit Hilfe der Gamma-Funktion ausgedrückt; das uneigentliche Integral wird durch geeignete Umformungen und Näherungen berechnet. Die Güte der Approximation wird nicht untersucht, aber es werden alle Rechenschritte erläutert und die Zwischenergebnisse veranschaulicht.
Die freie Energie F = U - TS ist die (negative) Legendre-Transformierte der inneren Energie U, wenn diese als Funktion der extensiven Variablen Entropie S und Volumen V dargestellt wird: U = U(S, V); die Legendre-Transformation wird dabei bezüglich der Variable S berechnet. Es ist dann leicht nachzuweisen, dass die freie Energie ein thermodynamisches Potential ist und dass die Änderung der freien Energie bei isothermen Zustandsänderungen mit der Zufuhr von mechanischer Arbeit übereinstimmt.
Mit Hilfe der freien Energie und der gebundenen Energie soll die innere Energie in zwei Anteile zerlegt werden: Die freie Energie soll allein durch die Zufuhr von mechanischer Arbeit und die gebundene Energie allein durch die Zufuhr von Wärme verändert werden. Diese Zerlegung lässt sich allerdings nur für isotherme Prozesse durchführen. Die Eigenschaften der freien und gebundenen Energie werden für die isotherme Zustandsänderung und andere einfache Prozesse diskutiert.
Mit dem Druckausgleich (also zwei Kammern mit einer beweglichen Trennwand, in der sich anfangs Gase mit unterschiedlichem Druck befinden) lassen sich zahlreiche Aspekte der Entropie und allgemeiner der Thermodynamik demonstrieren (reversible und irreversible Prozessführung, Eindeutigkeit des Endzustandes, Maximum der Entropie, Temperatur- und Volumenabhängigkeit der Entropie).
Wird die innere Energie als Funktion der extensiven Variablen dargestellt, enthält sie sämtliche Eigenschaften des entsprechenden thermodynamischen Systems; dies rechtfertigt die innere Energie als thermodynamisches Potential zu bezeichnen. Untersucht man speziell die innere Energie bei adiabatischen Zustandsänderungen, so kann man leicht motivieren, weshalb andere thermodynamische Potentiale (wie freie Energie oder Enthalpie) eingeführt werden. Am idealen einatomigen Gas werden diese Eigenschaften der inneren Energie demonstriert.
Der Carnot-Prozess ist sowohl inhaltlich als auch methodisch wichtig für die Thermodynamik: Seine Analyse liefert zahlreiche Einsichten in ihre Konzepte, Argumentationsweisen und technische Anwendungen.
Funktionsfabriken sind ein Konzept der funktionalen Programmierung. Damit werden Funktionen bezeichnet, die als Rückgabewert eine Funktion besitzen. Zum Einsatz von Funktionsfabriken sind Kenntnisse über die Umgebung einer Funktion nötig, um von der erzeugten Funktion auf die Variablen zuzugreifen, die innerhalb der Funktionsfabrik berechnet wurden. Es wird diskutiert, wann Funktionsfabriken eingesetzt werden sollen (ihr Einsatz ist niemals zwingend, da man sie immer durch herkömmliche Funktionen ersetzen kann). Beispiele, insbesondere mit Fabriken für quadratische Formen, werden ausführlich vorgestellt.
Die Legendre-Transformation wird geometrisch motiviert, indem die Menge der Tangenten an den Graphen einer Funktion betrachtet wird. Die formale Definition wird von der Verallgemeinerung, der Legendre-Fenchel-Transformation, abgegrenzt und es wird gezeigt, dass für differenzierbare und konvexe Funktionen beide Transformationen identisch sind. Für einfache Funktionen wird die Legendre-Transformation berechnet und veranschaulicht.
Für das ideale einatomige Gas werden die Zusammenhänge zwischen den Hauptsätzen der Thermodynamik und den Zustandsgleichungen (thermische und kalorische Zustandsgleichung) diskutiert und angewendet, um die Entropie in verschiedenen Darstellungen zu berechnen. Illustriert werden die Herleitungen an speziellen Zustandsänderungen (isotherm, isochor, adiabatisch, freie Expansion).
Die Jensensche Ungleichung liefert eine Abschätzung zwischen der Anwendung einer Funktion auf eine konvexe Kombination beziehungsweise der konvexen Kombination der Funktionswerte. Je nachdem, ob die Funktion konvex oder konkav ist, erhält man ein anderes Ungleichheitszeichen zwischen den genannten Termen. Im Folgenden werden die zum Beweis der Jensenschen Ungleichung nötigen Eigenschaften von konvexen Funktionen erläutert, die Jensensche Ungleichung formuliert und bewiesen und einige Anwendungen gezeigt (Ungleichung zwischen dem geometrischen und dem arithmetischen Mittel, Anwendung der Jensenschen Ungleichung auf Erwartungswerte von Zufallsvariablen).
Die Definition der Entropie eines Wahrscheinlichkeitsmaßes oder einer Zufallsvariable wird an einfachen Beispielen erläutert. Es wird diskutiert, dass die Entropie kein Streuungsmaß ist (wie die Standardabweichung), sondern die Ungewissheit (oder Unbestimmtheit) des Ausgangs eines Zufallsexperimentes beschreibt.
Die Funktion lm() ist ein mächtiges Instrument für die lineare Regression, das zahlreiche statistische Informationen über die untersuchten Daten bereitstellt. Es wird hier nur für die wichtigsten statistischen Größen gezeigt, wie man sie entweder direkt oder durch weitere Hilfsfunktionen gewinnen kann.
Durch Definition geeigneter Zufallsvariablen (Regressionswert und Residuum) bei einer Regressionsanalyse wird man auf die sogenannte Varianzzerlegung geführt. Sie erlaubt es durch eine einzige Kennzahl (das Bestimmtheitsmaß) zu beurteilen, wie gut die Messdaten durch die Regressionsgerade approximiert werden. Das Diagramm, das die Güte der Approximation am Besten ausdrücken kann, ist der Residualplot.
An zwei konkreten Beispielen wird gezeigt, wie aus stark beziehungsweise schwach korrelierten Messdaten die Regressionsgerade berechnet wird und wie man ihre Eigenschaften veranschaulichen kann. Herleitungen der Formeln zur Berechnung der Regressionskoeffizienten (Methode der kleinsten Quadrate) werden hier nicht gegeben; auch die Quelltexte zur den Berechnungen und Diagrammen werden hier nicht gezeigt.
Geometrische oder dynamische Probleme in drei Dimensionen, die eine Zylindersymmetrie oder Kugelsymmetrie besitzen, lassen sich besonders einfach mit Zylinderkoordinaten beziehungsweise Kugelkoordinaten beschreiben. Diskutiert werden deren Definition, die Koordinatenlinien und -flächen sowie die Basisvektoren. In den R-Skripten werden einige spezielle Eigenschaften näher untersucht und zugleich Beispiele gezeigt, wie dreidimensionale Graphiken mit scatterplot3d erstellt werden.
Das Paket scatterplot3d erleichtert die Darstellung von dreidimensionalen Punktwolken. Es bietet zudem zahlreiche Funktionalitäten, mit denen derartige Plots gehaltvoller gestaltet werden können, wie das Eintragen von zusätzlichen Punkten, Linien und Ebenen oder Konturlinien. An einigen speziellen Anwendungen wird ein Großteil dieser Funktionalitäten vorgestellt.
Mit ebenen Polarkoordinaten lassen sich geometrische oder dynamische Probleme besonders einfach beschreiben, wenn sie auf eine Ebene beschränkt und rotationssymmetrisch sind. (Das Paradebeispiel dafür ist die Kreisbewegung, die durch die Angabe des Kreisradius und des Drehwinkels anstelle der kartesischen Koordinaten nur eine veränderliche Größe besitzt.) Da die Koordinatenlinien Halbgeraden und Kreise sind, werden sie als krummlinige Koordinaten bezeichnet. Diskutiert werden die wichtigsten Eigenschaften, die Polarkoordinaten von kartesischen Koordinaten unterscheiden; die Vorgehensweise lässt sich dann leicht auf andere krummlinige Koordinatensysteme übertragen. Für den Umgang mit Polarkoordinaten wichtig ist der Zusammenhang zwischen der arctan-Funktion und der Berechnung des Azimutwinkels. In vielen Programmiersprachen wird dies durch die Funktion atan2() erleichtert, die man aber nur anwenden sollte, wenn man die Spitzfindigkeiten ihres Zusammenhangs zur arctan-Funktion kennt.
Die Methode, den Erwartungswert einer Zufallsvariable X mit Hilfe von Indikatorvariablen zu berechnen, ist deshalb so wichtig, weil man dazu die Verteilung von X nicht kennen muss. Die eigentliche Schwierigkeit besteht oft darin, geeignete Indikatorvariablen zu finden. An mehreren Beispielen (Münzwurf, hypergeometrische Verteilung und einer Zufallsvariable mit unbekannter Verteilung) wird dieses Vorgehen demonstriert. Da man Varianzen auf Erwartungswerte zurückführen kann, lassen sich mit dieser Methode auch Varianzen und Standardabweichungen berechnen.
Die hypergeometrische Verteilung beschreibt die Wahrscheinlichkeit dafür, dass beim Ziehen ohne Zurücklegen n Treffer aus einer Urne gezogen werden; dazu befinden sich in der Urne anfangs L Treffer und K Nieten und es werden N Lose entnommen. Die Abhängigkeit der Verteilung von den drei Parametern K, L und N erschwert den Zugang zur Berechnung der gesuchten Wahrscheinlichkeiten. Es werden zwei - natürlich gleichwertige - Methoden gezeigt, wie man die Wahrscheinlichkeiten berechnet.
Das Abzählproblem "Ziehen ohne Zurücklegen" wird unter der Annahme betrachtet, dass sich in der Urne zwei Arten von Objekten befinden (etwa K Nieten und L Treffer). Berechnet wird die Anzahl der möglichen Ergebnisse, wenn N-mal ein Los aus der Urne gezogen wird und dabei die Reihenfolge der Ergebnisse beachtet wird.
Ebenso wird gezeigt, wie man die möglichen Ergebnisse mit Hilfe des Hamming-Abstandes charakterisieren und mit Hilfe des N-dimensionalen Hyperwürfels und im Pascalschen Dreieck veranschaulichen kann. In den R-Skripten werden Algorithmen für das Abzählproblem und die Berechnung der möglichen Ergebnisse vorgestellt und diskutiert.
Binomialkoeffizienten und einige einfache Anwendungen in Abzählproblemen (wie die Anzahl der möglichen Ergebnisse beim Zahlenlotto) wurden bereits in den Begriffsbildungen der Kombinatorik vorgestellt. Hier werden die grundlegenden Eigenschaften der Binomialkoeffizienten diskutiert: die Pascalsche Rekursionsformel, der Aufbau des Pascalschen Dreiecks, der binomische Satz. Binomialkoeffizienten treten in unüberschaubar vielen Bereichen der Mathematik auf und ihr Auftreten sollte immer als Hinweis auf - mehr oder weniger offensichtliche - Querverbindungen verstanden werden. Als Beispiel einer dieser Querverbindungen wird der Zusammenhang der Binomialkoeffizienten mit dem n-dimensionalen Hyperwürfel diskutiert.
Es werden Simulationen zum Temperaturausgleich durchgeführt: Das Modellsystem mit äquidistanten Energieniveaus wird in zwei Teilsysteme zerlegt, die anfangs unterschiedliche Energie haben. Es entwickelt sich unter einer einfachen Dynamik, bei der zufällig zwei Moleküle ausgewählt werden, die ein Energiequant austauschen.
Die Ergebnisse der Simulationen sollen die Konzepte illustrieren, mit denen die statistische Mechanik einen irreversiblen Vorgang beschreibt, der in der phänomenologischen Thermodynamik als Paradebeispiel für den zweiten Hauptsatz dient.
Das p-Quantil als Umkehrfunktion der Verteilungsfunktion und der Spezialfall des Medians als p-Quantil zur Wahrscheinlichkeit p = 0.5 werden vorgestellt.
Das Modellsystem mit äquidistanten Energieniveaus wird mit einer einfachen Dynamik ausgestattet, die es erlaubt Energie zwischen zwei Molekülen auszutauschen. Damit lässt sich beobachten, welche Folge von Zuständen das System einnimmt, wenn man es in einem unwahrscheinlichen Mikrozustand startet. Die vorgestellten Simulationen und ihre Auswertung liefern weitere Illustrationen der Konzepte der statistischen Mechanik: Mikro- und Makrozustände, statistische Interpretation des zweiten Hauptsatzes der Thermodynamik.
Die Funktion sample() wird verwendet, um Stichproben zu erzeugen. Damit dies nicht zu unerwünschtem Verhalten führt, muss man wissen, dass der Aufruf an sample.int() weitergereicht wird, wenn die Menge, aus der ein Objekt ausgewählt werden soll, nur ein Element besitzt. Es wird ein Beispiel ausführlich besprochen, bei dem eine naheliegende Implementierung zu unerwarteten Ergebnissen führt.
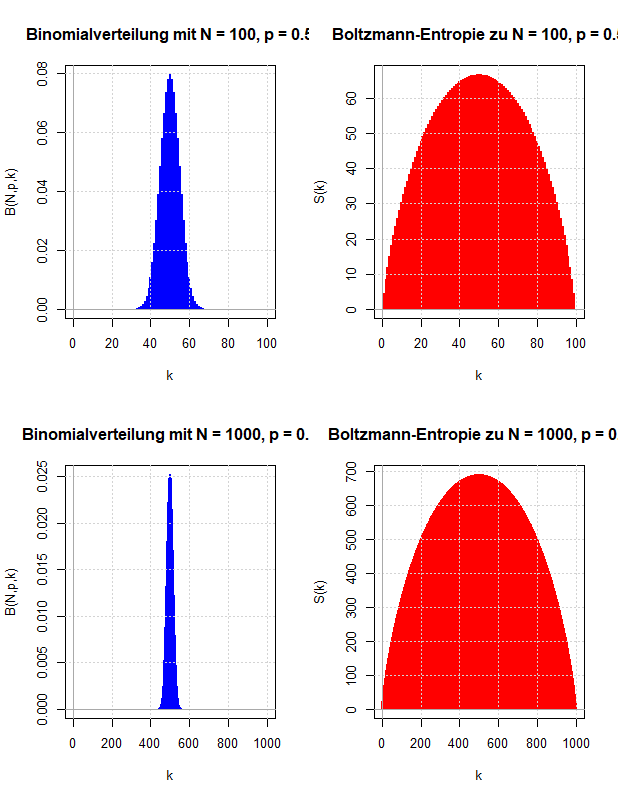
Die Konzepte Mikrozustand, Makrozustand, Gleichverteilungs-Postulat und Boltzmann-Entropie der statistischen Mechanik werden mit Hilfe einfacher Simulationen erläutert.
Für das Modellsystem mit unabhängigen Teilchen, die äquidistante Energieniveaus besitzen, werden die wichtigsten statistischen und thermodynamischen Größen berechnet.
Nach dem Postulat der statistischen Mechanik besitzen alle Mikrozustände, die ein System annehmen kann, die gleiche Wahrscheinlichkeit. Für zahlreiche Simulationen benötigt man einen Zufallsgenerator, der diese gleichverteilten Mikrozustände erzeugt. Dieser Zufallsgenerator wird in der Programmiersprache R entwickelt, die Erklärungen sind aber so allgemein gehalten, dass man sie leicht in eine andere Programmiersprache übersetzen kann.
In den vorausgegangenen Kapiteln wurden die Abzählprobleme behandelt, die sich ergeben, wenn ein thermodynamisches System entweder auf der Ebene der Mikrozustände oder der Makrozustände beschrieben wird. Vergleicht man diese Ergebnisse mit den Gleichungen der phänomenologischen Thermodynamik, kann man eine statistische Definition der Entropie ableiten und damit eine (statistische) Erklärung des zweiten Hauptsatzes der Thermodynamik liefern. Die Boltzmann-Entropie wird mit Hilfe der Anzahl der Mikrozustände pro Makrozustand definiert und besitzt die Eigenschaften, die man innerhalb der Thermodynamik an die Entropie stellt.
Die geometrische Verteilung wird verwendet, um Wartezeiten zu modellieren. Die grundlegenden Eigenschaften wie Erwartungswert, Varianz, Standardabweichung, die Verteilungsfunktion und insbesondere der Zusammenhang zur Binomialverteilung und die sogenannte Gedächtnislosigkeit werden besprochen.
Es werden zwei Anwendungen des Entropiesatzes besprochen. Zum Einen warum Wärme immer vom wärmeren zum kälteren Körper strömt und niemals umgekehrt. Zum Anderen die Entropieproduktion bei einem Mischvorgang. Dabei wird geklärt, für welchen Rechenschritt welcher Hauptsatz der Thermodynamik verwendet wird.
Für ein einfaches Modellsystem wird untersucht, welcher Makrozustand durch die meisten Mikrozustände realisiert wird und wie sich dieser Makrozustand charakterisieren lässt. Dabei werden die zugehörigen Abzählprobleme näherungsweise gelöst, da ihre exakte Lösung nur für sehr kleine Teilchenzahlen möglich ist. Die Methoden für diese Näherungen werden ausführlich besprochen: Stirling-Formel und Suche nach dem Maximum eines Multinomialkoeffizienten unter Nebenbedingung (mit Lagrange-Multiplikatoren).
Die statistische Mechanik versucht das makroskopische Verhalten von Materie zu erklären, indem anstelle einer detaillierten mikroskopischen Beschreibung Vergröberungen vorgenommen und statistische Methoden angewendet werden. Ein zentrales Konzept ist dabei die Definition von Makrozuständen, die Äquivalenzklassen auf der Menge der Mikrozustände erzeugen. Dieses Konzept und welche Abzählprobleme dabei entstehen, wird an einem einfachen Modellsystem erklärt.
Das Abzählproblem, nicht unterscheidbare Kugeln auf nicht unterscheidbare Urnen zu verteilen ist äquivalent zum Problem zu einer ganzen Zahl Z Zerlegung in L Summanden zu finden. Eine derartige Zerlegung wird als Partition bezeichnet. Wie viele Partitionen es gibt, wird für mehrere Fälle untersucht: Die Vertauschung der Reihenfolge zählt (oder zählt nicht) als neue Partition, die Null ist als Summand zugelassen, die Länge der Partition wird nicht festgelegt. Man kann für diese Abzählprobleme zwar Rekursionsformeln angeben, man kann mit einfachen Mitteln aber keine expliziten Formeln angeben, die die Rekursionsformeln lösen.
Kombinationen mit Wiederholungen treten in mehreren Abzählproblemen auf, die zunächst sehr unterschiedlich wirken. Es wird ihre Äquivalenz gezeigt und die Formel hergeleitet, wie man die Anzahl aller Kombinationen mit Wiederholungen berechnet. Dazu verwendet man die Methode Stars and Bars. In den R-Skripten wird ein einfacher Algorithmus gezeigt, wie man die Menge alle Kombinationen mit Wiederholungen rekursiv berechnet.
Die Funktion sample() wird verwendet, um Stichproben zu erzeugen. Sie lässt sich so konfigurieren, dass man die Wahrscheinlichkeitsverteilungen von beliebigen selbstdefinierten diskreten Zufallsvariablen einsetzen kann. Zudem kann man das Ziehen mit beziehungsweise ohne Zurücklegen realisieren.
Mit Hilfe von Zeigern kann man Funktionen realisieren, die Felder als Eingabewert beziehungsweise als Rückgabewert besitzen. Es ist sogar möglich, Zeiger auf Funktionen zu setzen und damit Funktionen als Eingabewerte anderer Funktionen einzusetzen.
Es werden einfache Aufgaben besprochen, die grundlegende Eigenschaften von Feldern und Zeigern behandeln und die man nach einem ersten Durchgang durch diese Themen beherrschen sollte.
Mit Funktionen lassen sich Quelltexte besser strukturieren und wiederkehrende Aufgaben können mit wenig Aufwand ausgeführt werden. Zur Syntax der Definition von Funktionen gehören ihre Deklaration (Funktionskopf), die Implementierung und ihr Aufruf aus anderen Funktionen heraus. Diese Bestandteile und wie man Deklaration und Implementierung im Quelltext anordnet, werden erklärt. Mehrere Aufgaben mit ausführlichen Lösungen dienen der Veranschaulichung.
Vorgestellt werden die Schleife mit Zählvariable (for-Schleife), die kopfgesteuerte Schleife (while-Schleife) und die fußgesteuerte Schleife (do-while-Schleife). Ihre Behandlung erfolgt aber nur exemplarisch an typischen Anwendungen. Eine detailliertere Behandlung findet sich im entsprechenden Kapitel zu C++.
Die wichtigsten Konzepte der Programmiersprache C werden an einfachen Programm-Beispielen erläutert: HelloWorld-Anwendung zum Testen der Arbeitsumgebung, Konsolenein- und ausgaben, Deklaration und Initialisierung von Variablen, arithmetische und logische Operationen, Ablaufsteuerung mit Bedingung und Alternative. Zudem werden einige methodische Hinweise gegeben, wie man gerade als Anfänger beim Programmieren strukturiert vorgehen sollte.
Inhalt und Lernziele des Kapitels Einführung in die Programmiersprache C und in C-Zeiger.
Die Faltung von Wahrscheinlichkeitsmaßen ist eine der wichtigsten Begriffsbildungen, um Summen von unabhängigen Zufallsvariablen zu beschreiben, da sich mit ihr viele Eigenschaften von Zufallsvariablen und Wahrscheinlichkeitsverteilungen prägnant formulieren lassen und zahlreiche Bezüge zu anderen (scheinbar entfernten) Begriffen und Aussagen herstellen lassen. In diesem einführenden Kapitel wird auf exakte mathematische Definitionen und Beweise verzichtet, stattdessen soll der Begriff der Faltung an typischen Beispielen motiviert werden.
Im dritten Teil über die Familie der apply-Funktionen werden zwei Gruppen von Funktionen vorgestellt: Zum Einen Funktionen für Wiederholungen (entweder Objekte oder Anweisungen), wodurch viele einfache Schleifen ersetzt werden können. Zum Anderen Funktionen, die Daten zuerst gruppieren und dann erst verarbeiten; hier werden zahlreiche Querverbindungen zu Dataframes und Faktoren hergestellt. Zur ersten Gruppe gehören rep() und replicate(), zur zweiten Gruppe ave(), by() und aggregate(), die alle sehr nahe verwandt sind mit tapply().
Nach dem Erwartungswert sind die Varianz und die Standardabweichung (als Wurzel der Varianz) die wichtigsten Kennzahlen einer Verteilung. Ist der Erwartungswert ein Maß für die Lage der Verteilung, beschreiben Varianz und Standardabweichung die Streuung der Werte einer Zufallsvariable um den Erwartungswert. Die Definition und Eigenschaften werden besprochen und an zahlreichen Beispielen erläutert.
Der Erwartungswert einer Zufallsvariable ist die wichtigste Kennzahl, um Ergebnisse von Zufallsexperimenten zu beschreiben. Seine Definition und Eigenschaften werden ausführlich erläutert. An zahlreichen Beispielen wird seine Berechnung vorgeführt; dabei werden nebenbei wichtige Wahrscheinlichkeits-Verteilungen vorgestellt.
Die Herleitung der Chernoff-Schranke beruht auf der momentenerzeugenden Funktion. Für den Spezialfall der Binomialverteilung kann die optimale Chernoff-Schranke explizit berechnet werden und es geht außer der Markov-Ungleichung keine weitere Näherung ein. Um die Vorgehensweise bei der Berechnung der Chernoff-Schranke besser verständlich zu machen, werden alle Herleitungsschritte besprochen und mit zahlreichen Diagrammen veranschaulicht.
Zu den wichtigsten Wahrscheinlichkeitsverteilungen gibt es Funktionen zum Berechnen der Wahrscheinlichkeitsdichte, der Verteilungsfunktion, des p-Quantils und zum Erzeugen von Zufallszahlen. Für ausgewählte Verteilungen (Binomialverteilung, Poisson-Verteilung, kontinuierliche Gleichverteilung und Normalverteilung) werden diese Funktionen vorgestellt. Dabei werden typische Anwendungen aus der Wahrscheinlichkeitsrechnung und Statistik gezeigt, die zugleich einige Eigenschaften dieser Verteilungen illustrieren.
Dar Datentyp Tabelle (table) wird verwendet, um Kontingenz-Tabellen zu erzeugen und auszuwerten. Einfachere Anwendungen, um die levels in einem Faktor zu zählen, wurden bereits in den Kapiteln über Faktoren beschrieben.
Inhalt und Lernziele des Kapitels Zusammengesetzte Datentypen in R.
Inhalt und Lernziele des Kapitels Einfache Datentypen in R.
Zufallsvariablen können diskrete oder kontinuierliche Werte annehmen. Die mathematische Beschreibung unterscheidet sich, da die Wahrscheinlichkeiten der Werte der Zufallsvariable entweder mit Folgen oder indirekt über eine Wahrscheinlichkeitsdichte angegeben werden. Diese Beschreibung wird an speziellen Verteilungen demonstriert: diskrete Gleichverteilung, Poisson-Verteilung, kontinuierliche Gleichverteilung, Standard-Normalverteilung.
Die Tschebyscheff-Ungleichung als einfachste Konzentrations-Ungleichung wird aus mehreren Perspektiven beleuchtet: Es werden Beispiele für ihre typische Anwendung besprochen; es wird ein direkter Beweis gegeben; es wird gezeigt, dass sie als Spezialfall der verallgemeinerten Markov-Ungleichung aufgefasst werden kann; es wird diskutiert, wie gut die Abschätzung ist, die sie liefert. In den R-Skripten werden die Berechnungen aus den Anwendungsbeispielen ausgeführt, die man ohne Programmierung kaum bewältigen könnte.
Zufallsvariablen sind die geeignete Begriffsbildung um sowohl Ereignisse als auch deren Wahrscheinlichkeiten treffend zu beschreiben und zu berechnen. In späteren Anwendungen der Wahrscheinlichkeitsrechnung werden Zufallsvariablen ständig eingesetzt. Hier wird zunächst gezeigt, wie Zufallsvariablen mit der Ereignisalgebra und dem Wahrscheinlichkeitsmaß zusammenhängen und sich so nahtlos in den Aufbau der Wahrscheinlichkeitsrechnung einfügen. In den R-Skripten wird gezeigt, wie man Zufallsvariable leicht modellieren kann.
Ein Algorithmus zur Simulation von N Spielen am k-armigen Banditen (multi-armed bandit) wird in R implementiert. Der Algorithmus erlaubt die Auswahl einer Strategie zur Wahl des nächsten zu spielenden Armes. Als Strategien stehen die im Artikel "Der mehrarmige Bandit (multi-armed bandit): Simulationen mit einfachen Algorithmen vorgestellten Strategien zur Auswahl, es können aber leicht weitere Strategien implementiert und eingefügt werden.
Um beim Spiel am mehrarmigen Banditen einen möglichst hohen Gewinn zu erzielen, benötigt man eine Strategie, die einen Kompromiss zwischen Exploration und Exploitation herstellt. Es werden einfache Algorithmen vorgestellt, die dieses Problem lösen und ihre Eigenschaften werden mit Hilfe von Simulationen untersucht.
Kleiner Ratgeber mit methodischen Hinweisen zum Selbststudium.
Beim mehrarmigen Banditen oder genauer k-armigen Banditen kann man ein Glücksspiel durch Betätigen eines Armes auslösen. Mathematisch modelliert werden sie durch Zufallsvariablen mit unterschiedlichen Erwartungswerten. Möchte man am k-armigen Banditen N Spiele durchführen und dabei einen möglichst hohen Gewinn erzielen, gerät man in ein Dilemma: Einerseits muss man alle Arme untersuchen, um ihre Kennzahlen zu schätzen (Exploration), andererseits möchte man möglichst oft den besten Arm betätigen (Exploitation). Im nächsten Kapitel werden dann Algorithmen entwickelt, die versuchen einen Kompromiss zwischen Exploration und Exploitation herzustellen.
Ein wichtiger Bestandteil des Monte-Carlo-Tree-Search-Algorithmus ist es, aus einer gegebenen Spielsituation zahlreiche Spiele auszuführen, bei denen die Züge zufällig ausgewählt werden. Die Ergebnisse dieser Simulationen bestimmen dann, wie der Algorithmus den Spielbaum weiter untersucht. Um besser nachvollziehen zu können, wie der Monte-Carlo-Tree-Search-Algorithmus den Spielbaum untersucht und für die möglichen Züge Gewinn-Wahrscheinlichkeiten schätzt, werden für das Zahlenspiel 3-5-11 die Formeln hergeleitet, wie man zu gegebenem Anfangswert die Gewinn-Wahrscheinlichkeit berechnen kann, wenn sämtliche Züge eines Spiels zufällig ausgewählt werden (mit jeweils gleicher Wahrscheinlichkeit). Ferner werden Simulationen mit unterschiedlichen Anzahlen von Spielen durchgeführt, um zu beurteilen, wie gut die Ergebnisse der Simulation mit den berechneten Gewinn-Wahrscheinlichkeiten übereinstimmen.
Als weitere Methode zur Lösung von Abzählproblemen wird die Rekursion vorgestellt. Dies geschieht am Beispiel eines Zahlenspiels, für das der vollständige Spielbaum entwickelt wird. Dieser wirkt zwar sehr unregelmäßig und kann mit den bekannten kombinatorischen Formeln nicht bewältigt werden, aber aufgrund seiner rekursiven Struktur lassen sich Abzählprobleme auf das Aufstellen der Rekursionsformel und der Behandlung des Basisfalls zurückführen.
Um die Vorgehensweise beim Monte-Carlo-Tree-Search-Algorithmus besser erklären zu können, wird zunächst ein einfaches Zahlenspiel vorgestellt und analysiert. Es handelt sich um eine Variation des Nim-Spiels, für das man eine einfache Gewinnstrategie angeben kann und bei dem mit dem Anfangswert bereits festgelegt ist, welcher Spieler den Gewinn erzwingen kann. Dies hat den Vorteil, dass man später besser nachvollziehen kann, wie der Monte-Carlo-Tree-Search-Algorithmus vorgeht.
Programmieraufgaben zur Anwendung von Feldern und Zeigern, die im Sinne der strukturierten Programmierung zu lösen sind. Die Quelltexte sollen in reinem C geschrieben werden, also keine Konzepte verwenden, die nur in C++ verfügbar sind.
Was zeichnet das Buch aus? Die Entdeckungsreise von Matoušek und Nešetřil will so gar nicht in die üblichen Kategorien von Mathematik-Büchern passen: Es gibt Lehrbücher, die streng nach dem Prinzip Definition – Satz – Beweis aufgebaut sind und die den Leser meist mit der Frage zurücklassen: "Wie soll ich jemals derartige Mathematik selber machen?" Und es gibt populärwissenschaftliche Bücher, die viel zu oberflächlich sind, um mit ihnen eigene mathematische Fähigkeiten entwickeln zu können. Warum ordnet sich die Entdeckungsreise hier nicht ein? Einerseits enthält es Definitionen, Sätze und Beweise und ein Blick in das Inhaltsverzeichnis erweckt den Eindruck eines üblichen Lehrbuches, andererseits findet man beim zufälligen Aufschlagen immer wieder Passagen im Plauderton . Dennoch ist es alles andere als eine Mischung der beiden genannten Kategorien. Um dies festzustellen, reicht es ein Kapitel zu lesen, von dem man glaubt, es schon gut zu kennen – selbst dort wird man...
Felder werden durch Zeiger organisiert und es ist gerade ein Charakteristikum der Sprache C, dass dies nicht nur intern verwendet wird, sondern dass man diesen Mechanismus selbst nutzen kann. Für den Einsteiger ist dies meist mit Schwierigkeiten verbunden, da man oft nicht entscheiden kann, mit welchem Objekt man gerade arbeitet (Zeiger oder Variable eines fundamentalen Datentyps). Die meisten der mit Feldern verbundenen Schwierigkeiten wie etwa die Zeigerarithmetik, die Ausgabe und der Vergleich von Feldern werden erklärt. Wie man Felder an Funktionen übergibt oder als Rückgabewert zurückerhält, wird im nächsten Kapitel erläutert.
In einem Feld werden mehrer Komponenten von gleichem Datentyp zu einem Objekt zusammengefasst. Die Anzahl der Komponenten muss bei der Deklaration angegeben werden und darf sich während der Laufzeit des Programmes nicht ändern. Der häufigste Fehler beim Umgang mit Feldern besteht im Zugriff auf Komponenten jenseits des deklarierten Bereichs, was zu unbestimmtem Verhalten des Programmes führen kann. Die unterschiedlichen Möglichkeiten zur Initialisierung eines Feldes werden vorgestellt. Felder können in beliebig vielen Dimensionen angelegt werden; besprochen werden hier nur eindimensionale Felder (Vektoren) und zweidimensionale Felder (Matrizen).
Zeiger sind Variable, deren Wert eine Adresse ist. Man kann sie mit der Adresse einer anderen Variable initialisieren. Da unterschiedliche Datentypen unterschiedlich großen Speicherplatz belegen, muss bei der Deklaration eines Zeigers angegeben werden, welchen Datentyp die Variable besitzt, auf deren Speicherplatz er verweist. Diese Eigenschaften von Zeigern und mit welchen Operatoren (Adressoperator, Indirektionsoperator) dies realisiert wird, wird hier ausführlich diskutiert. Als Anwendung wird gezeigt, wie man mit Zeigern Funktionen realisieren kann, die mehrere Rückgabewerte besitzen.
Das Damenproblem, also die Aufgabe möglichst wenige Damen auf einem Schachbrett so aufzustellen, dass das gesamte Schachbrett beherrscht wird, wird in ein Problem der Graphentheorie übersetzt. Zu dessen Lösung wird ein brute-force-Algorithmus entwickelt, der darauf beruht, dass man das Schachbrett mit einer Adjazenz-Matrix beschreibt und diese geeignet auswertet.
Die Funktion lapply() ersetzt eine Iteration über die Komponenten einer Liste, wobei auf jede Komponente eine Funktion FUN angewendet wird; die Rückgabewerte werden wieder zu einer Liste zusammengefasst. Entsprechend wird mit mapply() über mehrere Listen iteriert, wobei in jedem Schritt entsprechende Komponenten ausgewählt werden und darauf wird die Funktion FUN angewendet. Die Funktion Map() ist ein Wrapper für mapply(), der die wichtigsten Anwendungsfälle abdeckt. Die meisten Funktionen in R sind vektorisiert, können also nicht nur auf einen Eingabewert, sondern auf einen Vektor angewendet werden. Die Vektorisierung von Funktionen ist ein in R zentrales Konzept, das ein besseres Verständnis der Funktion mapply() liefert. Zuletzt wird die Funktion outer() mit einigen Anwendungen besprochen. Die Funktion outer() besitzt zwei Vektoren (oder Felder) als Eingabewert und baut daraus ein komplexeres Feld auf.
In der Familie der apply-Funktionen gibt es mehrere Vertreter, mit den über die Elemente einer Liste iteriert werden kann, wobei auf jede Komponente eine Funktion f() angewendet wird. Besprochen werden lapply(), sapply(), vapply() und rapply(). Die Funktion lapply() ist dabei der grundlegende Vertreter, der die bei der Iteration entstehenden Rückgabewerte wieder zu einer Liste zusammensetzt. Dagegen versucht sapply() einen möglichst einfachen Rückgabewert zu erzeugen (Vektor oder Feld). Der Funktion vapply() kann eine Vorlage für den Rückgabewert übergeben werden, so dass man bessere Kontrolle für weitere Berechnungen hat. Mit rapply() können bestimmte Datentypen aus einer Liste selektiert werden und nur auf diese wird die Funktion f() angewendet; zudem wird die Anwendung von f() rekursiv an die Komponenten der Liste weitergereicht.
Die Funktion apply() erlaubt es, über die Zeilen beziehungsweise Spalten einer Matrix zu iterieren und dabei eine Funktion FUN auf die Zeilen oder Spalten anzuwenden. Dabei entstehen leichter verständliche Quelltexte als bei den gleichwertigen Schleifen. Die Arbeitsweise der Funktion apply() kann man in drei Phasen unterteilen: split, apply, combine (Aufspalten der Matrix, Anwenden der Funktion FUN auf die Teile, Zusammensetzen der einzelnen Rückgabewerte zum Rückgabewert von apply()). Diese drei Phasen werden ausführlich erklärt und damit die Diskussion weiterer mit apply() verwandter Funktionen vorbereitet.
Bisher wurden für alle Datentypen Diagnose-Funktionen vorgestellt, die über Form und Inhalt von Objekten Aufschluss geben. Für Funktionen gibt es ebenso eine Reihe von Diagnose-Funktionen, die zu weiteren Konzepten der objekt-orientierte und funktionale Programmierung führen oder spezielle Konzepte von R betreffen. Vorgestellt werden die wichtigsten Diagnose-Funktionen für Funktionen, wobei nicht alle weiterführenden Konzepte im Detail besprochen werden können.
Erläutert wird die Syntax, mit der man spezielle Funktionen in R selbst definieren kann: Funktionen mit dem Argument dot-dot-dot ("..."), binäre Operatoren, Funktionen höherer Ordnung und Funktionale, anonyme Funktionen, Listen von Funktionen, replacement-Funktionen, Funktionen mit unsichtbarem Rückgabewert. Um erste Funktionen in R zu implementieren reichen die Kenntnisse aus den Kapiteln Eigenschaften von Funktionen in R und Selbstdefinierte Funktionen in R (UDF = User Defined Functions); möchte man R tatsächlich als funktionale Programmiersprache nutzen, sind die hier vermittelten Kenntnisse unerlässlich.
Die Programmiersprache R bietet eine unüberschaubare Vielzahl von Funktionen, die bereits in den Standard-Paketen enthalten sind. Dennoch ist es unerlässlich, selber Funktionen zu implementieren, um selbstgestellte Aufgaben übersichtlich abzuarbeiten. Vorgestellt werden zwar nicht alle, aber die wichtigsten Hilfsmittel und Techniken für selbstdefinierte Funktionen: Die Syntax der Definition einer Funktion, Besonderheiten des Rückgabewertes einer Funktion, die Prüfung der Eingabewerte einer Funktion, das Setzen von default-Werten für die Argumente einer Funktion und einiges über den Mechanismus, wie Funktions-Argumente übergeben werden (call by value).
Eine Funktion ruft einen Quelltext-Abschnitt auf, der durch Eingabewerte konfiguriert werden kann und der einen Rückgabewert berechnet. Allgemeine Eigenschaften und Besonderheiten über die Eingabewerte und den Rückgabewert einer Funktion werden besprochen. Dies soll auf das nächste Kapitel vorbereiten, in dem gezeigt wird, wie man Funktionen selbst definiert.
Die while-Schleife und die repeat-Schleife sind etwas allgemeiner als die for-Schleife. Wenn man weiß, wie oft eine Schleife durchlaufen werden soll, ist die for-Schleife weniger fehleranfällig einzusetzen. Ist dagegen nur die Bedingung bekannt, unter die Schleife verlassen werden soll, muss man die while- oder repeat-Schleife einsetzen. Die while-Schleife realisiert die kopfgesteuerte Schleife, die repeat-Schleife besitzt keine Bedingungsprüfung. Wie bei der for-Schleife können die Schlüsselwörter break (vorzeitiges Verlassen der Schleife) und next (sofortiger Übergang zum nächsten Schleifen-Durchlauf) eingesetzt werden.
Schleifen mit einer Zählvariable werden eingesetzt, wenn bekannt ist, wie oft ein gewisser Vorgang wiederholt werden muss (wobei die Anweisungen nicht exakt identisch sind, sondern meist vom Wert der Zählvariable abhängen). Die Syntax der for-Schleife sowie einige mit ihr verbundene Spitzfindigkeiten werden erklärt. Zusätzliche Kontrolle über den Ablauf einer Schleife erhält man durch break (vorzeitiges Verlassen der Schleife) und next (sofortiger Übergang zum nächsten Wert der Zählvariable).
Die Mehrfachalternative lässt sich durch verschachtelte Alternativen realisieren, was aber oft zu umständlichen und fehleranfälligen Quelltexten führt. Übersichtlicher ist die Realisierung mit der Funktion switch(). Für sie gibt es in R zwei Versionen, die sich in der Bedingungsprüfung unterscheiden: entweder wird eine Zeichenkette ausgewertet (character-Version) oder das Ergebnis der Bedingungsprüfung wird in eine ganze Zahl verwandelt (integer-Version).
Die Bedingungsprüfung mit if und die Alternative mit if else sind die wohl am häufigsten eingesetzten Kontrollstrukturen, durch die sich der Ablauf eines Programmes steuern lässt – sie sorgen dafür, dass gewisse Programm-Teile nur ausgeführt werden, wenn eine bestimmte Bedingung erfüllt ist. In R gibt es zusätzlich eine vektorisierte Variante der Alternative mit ifelse().
Nach den grundlegenden Eigenschaften im Kapitel "Dataframes in R: der Datentyp data frame" werden jetzt Anwendungen von Dataframes gezeigt: der Zugriff auf ein Dataframe (auf Spalten, Zeilen, einzelne Elemente oder Teilmengen), Sortierung eines Dataframes, Daten-Aggregation, Umwandlung in eine Matrix sowie das Schreiben eines Dataframes in eine Datei und umgekehrt das Lesen von tabellarischen Daten aus einer Datei.
Der Datentyp Dataframe vereinigt viele Eigenschaften der Datentypen Matrix und Liste und ist in zahlreichen Anwendungen der geeignete Rahmen, um statistische Daten zu speichern und ihre Auswertung vorzubereiten. Der erste Teil über Dataframes zeigt, wie man sie erzeugen und ihre Eigenschaften abfragen kann (Diagnose-Funktionen). Im nächsten Kapitel werden Anwendungen von Dataframes gezeigt.
In der Statistik muss man oft Daten gruppieren und die gruppierten Daten auswerten. In R wird eine derartige Gruppierung mit einem Faktor (oder mehreren Faktoren) vorgenommen. Das Kapitel beschreibt R-Funktionen, die diese Aufgaben erleichtern, und zeigt ihre praktische Anwendung.
Ausgehend von der Frage, welcher Zusammenhang zwischen Multiplikationstabellen und Linearkombinationen in den ganzen Zahlen bestehen, werden der Euklidische Algorithmus und seine Erweiterung besprochen. Der Euklidische Algorithmus berechnet den größten gemeinsamen Teiler zweier Zahlen, der erweiterte Euklidische Algorithmus erlaubt es zusätzlich, den größten gemeinsamen Teiler von a und b als Linearkombination von a und b darzustellen. Die Analyse dieser Algorithmen liefert zahlreiche Einsichten in die Zusammenhänge zwischen Kongruenzen, Linearkombination in Z und den Eigenschaften des größten gemeinsamen Teilers zweier Zahlen. In den R-Skripten werden Implementierungen vorgestellt sowie Verbesserungen (Blankinship, Stein) des Euklidischen Algorithmus diskutiert.
Die Eigenschaften der Teilbarkeitsrelation werden untersucht. Besonders ausführlich wird gezeigt, dass sie eine Ordnungsrelation ist, welche Eigenschaften Ordnungsrelationen haben und wie sich diese in einem Hasse-Diagramm darstellen lassen. In den R-Skripten wird gezeigt, wie man das Hasse-Diagramm für eine beliebige Ordnungsrelation erzeugt. Die Anwendungsbeispiele zeigen dann Zusammenhänge zwischen der Teilbarkeitsrelation, der Teilmengenrelation und der Primfaktorzerlegung.
Die Addition und die Multiplikation sind invariant gegenüber der Restklassenbildung. Aus dieser Tatsache lassen sich leicht die Teilbarkeitsregeln herleiten, mit denen man schnell entschieden kann, ob eine Zahl z durch eine andere Zahl k geteilt werden kann oder welcher Rest bei der Division bleibt.
Die Ganzzahl-Division (oder Division mit Rest) führt zu wichtigen Begriffsbildungen: Kongruenz, Restklassen und ihre Verallgemeinerungen Äquivalenzrelation und Äquivalenzklassen. Insbesondere kann mit einer Äquivalenzrelation eine Zerlegung der zugrundeliegenden Menge definiert werden.
In der Statistik steht man oft vor der Aufgabe, eine Reihe von Messdaten zu klassifizieren (oder: gruppieren) und die gruppierten Daten weiter auszuwerten (etwa Häufigkeiten der Klassen feststellen, Mittelwertbildung innerhalb der Klassen). Man kann diese Operationen natürlich auf der Ebene von Vektoren durchführen, indem man geeignete Funktionen für Vektoren anwendet. In R gibt es den Datentyp factor, der die Klassifizierung vornimmt und zahlreiche Auswertungen deutlich vereinfacht. Vorgestellt werden hier zuerst die Begriffe aus der Statistik, die mit der Klassifizierung von Daten zusammenhängen; weiter wie Faktoren und geordnete Faktoren erzeugt werden sowie deren Eigenschaften. Im folgenden Kapitel werden dann Anwendungen mit Faktoren gezeigt.
Die fundamentalen Begriffe der Wahrscheinlichkeitsrechnung, nämlich Ereignisalgebra, Wahrscheinlichkeit, Wahrscheinlichkeitsraum und die Axiome von Kolmogorov, werden formuliert. Es werden einige einfache Anwendungen und Skripte für Simulationen von Zufallsexperimenten gezeigt.
Die grundlegenden Begriffe der Wahrscheinlichkeitsrechnung werden eingeführt: Zufallsexperiment, Ergebnismenge, Ereignis, Ereignisalgebra, Wahrscheinlichkeit und Wahrscheinlichkeitsraum. Ferner werden Computer-Experimente zum Vergleich der Wahrscheinlichkeit und der relativen Häufigkeit vorgestellt.
Nachdem im letzten Kapitel Beispiele für einfache Abzählprobleme vorgestellt wurden, werden jetzt die Grundbegriffe der Kombinatorik, nämlich Variation, Permutation und Kombination eingeführt, systematisch untersucht und an weiteren einfachen Beispielen erläutert.
An einfachen Abzählproblemen beim Würfeln wird gezeigt, wie man in der Kombinatorik systematisch vorgeht, um Abzählprobleme zu klassifizieren und allgemeine Formeln zur Berechnung der Anzahl der Realisierungen gewisser Ereignisse herzuleiten. In den R-Skripten werden Beispiele gezeigt, wie man solche Probleme auch ohne Kenntnisse aus der Kombinatorik mit roher Gewalt (brute force-Algorithmen) lösen kann.
Die Inhalte Ungewohnt für ein Lehrbuch ist die – fast schon essaystische – Anordnung der Kapitel. Inhaltlich kann man sie völlig getrennt voneinander lesen; zusammengehalten werden sie durch die Einheitlichkeit des Gesamtthemas Mathematik und Technologie und die dabei verwendete Methodik. Für ...
Übersicht über die in drei weiteren Artikeln ausführlich besprochenen interaktiven Elemente für HTML-Seiten.
Für das Schach-Programm Fritz von ChessBase wird gezeigt, wie es in eine HTML-Seiten integriert werden kann.
Der pgn-Viewer von ChessBase kann verwendet werden, um Live-Übertragungen von Schach-Turnieren in einer HTML-Seite anzuzeigen.
Für die pgn-Viewer von Chess Tempo und ChessBase wird gezeigt, wie sie in HTML-Seiten integriert werden und welche weiteren Konfigurationsmöglichkeiten bestehen.
Übersicht über interaktive Elemente, um auf HTML-Seiten Schach-Aufgaben darzustellen.
Für die besprochenen Elemente werden Einbau-Anleitungen und Probeseiten gezeigt.
Was sind die besonderen Vorzüge des Buches? Die Vorteile als Mathematik -Buch seien kurz genannt: Die komplette Mathematik für ein Informatik-Studium ist enthalten: natürliche Zahlen, algebraische Strukturen, Zahlentheorie reelle und komplexe Zahlen Lineare Algebra Graphentheorie ...
In Stellenwertsystemen bildet man Zahlen, indem man Ziffern je nach ihrer Position mit einer Potenz der Basis gewichtet. Vorgestellt wird die allgemeine Definition eines Stellenwertsystems und die wichtigsten Vertreter: Dezimalsystem, Hexadezimalsystem, Dualsystem und Oktalsystem. Mir R-Skripten wird die Umrechnung zwischen Zahlensystemen durch eine Rekursion realisiert.
Funktionen aus den Basis-Paketen von R werden besprochen, mit denen Listen verarbeitet werden können. Insbesondere wird dabei auf die rekursive Struktur von Listen eingegangen.
Listen sind in R die grundlegende rekursive Struktur: anders als bei einem Vektor, bei dem alle Komponenten einen identischen Datentyp besitzen müssen, ist für die Komponenten einer Liste ein beliebiger Datentyp zulässig - sie können sogar selber wieder Listen sein.
Vorgestellt werden Funktionen zum Erzeugen von Listen, der Zugriff auf die Komponenten einer Liste, Diagnose-Funktionen für Listen und das Attribut names.
Es werden die Eigenschaften von primitiven pythagoreischen Zahlentripeln gezeigt und die Sätze bewiesen, die angeben, wie man alle primitiven pythagoreischen Zahlentripel explizit berechnen kann.
Zusammenstellung verschiedener Kapitel der Mathematik, die insbesondere für Programmierer, Informatiker, Ingenieure und Naturwissenschaftler relevant sind. Kurs zum Selbststudium.
Der Satz des Pythagoras ist zunächst eine geometrische Aussage über die Seitenlängen eines rechtwinkligen Dreiecks. Da es aber einige Dreiecke mit ganzzahligen Seitenlängen gibt (pythagoreische Zahlentripel) führt er schnell zu Fragen der Zahlentheorie. Einige Beweise des Satzes werden vorgestellt und es werden die Bezeichnungen für die zahlentheoretischen Fragestellungen eingeführt (näher untersucht werden sie in den anschließenden Kapiteln).
Felder sind in R die Verallgemeinerung von Matrizen. In einer Matrix werden die Komponenten zweidimensional angeordnet (Zeilen und Spalten), in einem Feld sind beliebige Dimensionen zugelassen. Erzeugt werden Felder meist, indem ein Vektor mit Hilfe des Dimensionsvektors mehrdimensional angeordnet wird, oder mit der Funktion outer(). Weitere Gemeinsamkeiten und Unterschiede zu Matrizen werden diskutiert.
Vorgestellt wird, wie Matrizen miteinander verknüpft werden, welche Funktionen Eigenschaften von Matrizen anzeigen, sowie zahlreiche Funktionen aus der Linearen Algebra (Berechnung von Determinanten, Lösung von linearen Gleichungssystemen, Berechnung von transponierten und inversen Matrizen, Berechnung von Eigenwerten und Eigenvektoren).
Die Komponenten eines Vektors können in R zweidimensional angeordnet werden wie in einer Matrix. Es werden verschiedene Möglichkeiten gezeigt, wie man Matrizen erzeugen kann, wie man spezielle Matrizen erzeugt und wie man auf die Komponenten einer Matrix zugreift. Weiter werden der Dimensionsvektor (Attribut dim) und das optionale Attribut dimnames vorgestellt. Wie Matrizen verknüpft werden und weitere Anwendungen folgen im nächsten Kapitel (Matrizen in R: Anwendungen).
Grundlegend für das Verständnis von Operationen, die mit Vektoren ausgeführt werden können, sind die punktweise Ausführung (eine Operation wird an die Komponenten weitergereicht) und der recycling-Mechanismus, der festlegt, wie Vektoren mit unterschiedlichen Längen verknüpft werden. Ausgehend hiervon werden zahlreiche Operationen vorgestellt, die mit Vektoren ausgeführt werden können (wie zum Beispiel statistische Funktionen, Sortier-Algorithmen, Mengen-Operationen).
Da es in R eigentlich keine fundamentalen Datentypen gibt (wie ganze Zahlen, Gleitkommazahlen, Zeichen, logische Werte), sondern diese Spezialfall eines Vektors der Länge 1 sind, ist dieses Kapitel entscheidend für das Verständnis von R. Vektoren bestehen aus Komponenten mit identischem Speichermodus und die Komponenten sind numeriert (oder wie man auch sagt: indiziert).
Vorgestellt werden hier Funktionen zum Erzeugen von Vektoren, der Zugriff auf die Komponenten eines Vektors, Diagnose-Funktionen für Vektoren und das Attribut names. Wie man Vektoren verknüpft und welche weiteren Funktionen zur Weiterverarbeitung von Vektoren existieren, wird im nächsten Kapitel gezeigt (Vektoren in R: Anwendungen).
Gezeigt wird, wie man in R die Zahlenbereiche für die Modi integer und double feststellen kann und wie man Zahlen in Potenz-Schreibweise eingeben kann. Ausführlich werden die Ausnahme-Werte Inf (Infinity), NaN (Not a Number), NA (Not Available) und NULL vorgestellt.
In R sind Zeichen kein fundamentaler Datentyp; sie werden nicht von Zeichenketten unterschieden. Um aber mit den Besonderheiten der Verarbeitung von Zeichen vertraut zu werden, werden vorerst nur Zeichen behandelt. Diese Besonderheiten betreffen insbesondere die Maskierung von bestimmten Zeichen und die Typumwandlungen. Einige harmlose Beispiele für Zeichenketten (die ohne Wissen über Vektoren verständlich sind) werden hier schon angeführt.
Übersicht über die folgenden Abschnitte, in denen die Komponenten des von Neumann-Rechners sowie die dazu nötigen elektrotechnischen Grundlagen behandelt werden.
Der Abschnitt behandelt die für den von Neumann-Rechner, insbesondere den Prozessor, relevanten elektrotechnischen Grundlagen:
Einführung in die Digitaltechnik, Transistoren, Schaltnetze und Schaltwerke.
Die Aufgaben des Betriebssystems haben sich im Lauf der Zeit gewandelt:
Anfangs war ein menschlicher Operator dafür zuständig, Programme zu starten und zu beenden, später wurde diese und weitere Aufgaben von Dienst-Programmen übernommen.
Um die Aufgaben und die Arbeitsweise des Betriebssystem besser zu verstehen, wird ein Computer in Schichten zerlegt: Anwendersoftware, Systemsoftware und Hardware.
Die wichtigsten Einteilungskriterien für Rechnernetze werden vorgestellt.
Aufgaben zum Selbststudium zum Kapitel Rechnerarchitektur.
Vorgestellt werden Festplatten als die wichtigsten externen Geräte eines von Neumann Rechners.
Ausführlich besprochen werden Aufbau und Funktionsweise der unterschiedlichen Arten von Festplatten .
Vorgestellt wird, wie der Hauptspeicher vom Prozessor über die Schnittstelle Adressregister und Datenregister angesprochen wird.
Der Hauptspeicher kann als statischer oder dynamischer Speicher realisiert sein (SRAM oder DRAM).
Für den Computer werden komplexe Operationen auf elementare Rechenoperationen heruntergebrochen. Deren wichtigste Gruppe sind logische Operationen, die hier ausführlich vorgestellt werden.
Vorgestellt wird die von Neumann Rechnerarchitektur und die wichtigsten Kenngrößen, die die Komponenten eines Computers charakterisieren.
Programmiersprachen werden eingesetzt, um Algorithmen zu schreiben.
Auszeichnungssprachen sind dazu da, um die Elemente eines Textes (wie Überschriften, Fließtext, Listen und dergleichen) logisch auszuzeichnen und meist Formatierungsregeln für diese Elemente festzulegen.
Als Beispiele für Auszeichnungssprachen werden LaTeX, HTML, XML und SVG vorgestellt.
Der Vorteil einer Auszeichnungssprache ist, dass sie sowohl menschen-lesbar als auch maschinen-lesbar ist, wodurch sie insbesondere in der automaischen Textverarbeitung eingesetzt wird.
Die Maschinensprache-Befehle sind noch nicht die elementaren Anweisungen für die Komponenten des Prozessors:
einen Maschinensprache-Befehl zu dekodieren heißt, ein Mikro-Programm zu laden, das den Befehl implementiert.
Je nach Prozessor-Architektur gibt es eine unterschiedlich große semantische Lücke zwischen den Maschinensprache-Befehlen und den Mikro-Befehlen.
Mit der Kenntnis der Mikro-Programme wird leichter verständlich, wie die Komponenten des Prozessors zusammenarbeiten und sie mit Hilfe des Pipelining optimal ausgelastet werden können.
Anwendungen aus verschiedensten Bereichen, in denen die bisher erlernten Konzepte von C++ eingesetzt werden können, werden als Programmier-Aufgaben formuliert.
Zu Aufgaben, die zu längeren Algorithmen führen, in denen insbesondere Bedingungs-Prüfungen und Alternativen vorkommen, werden einige Lösungshinweise gegeben.
Bedingung, Alternative und Mehrfachalternative sind die Kontrollstrukturen, die man einsetzen kann, um den Ablauf eines Programmes zu steuern.
Erklärt wird ihre Syntax in C++ und es werden einige Spitzfindigkeiten diskutiert, die man bei ihrer Verwendung kennen sollte.
Für das Erlernen der Sprache C++ ist dieser Abschnitt zentral: es werden die wichtigsten fundamentalen Datentypen ausführlich vorgestellt, also Zeichen, Boolesche Variable, ganze Zahlen und Gleitkommazahlen. Die Datentypen sind immer verknüpft mit den Operationen, die mit ihnen ausgeführt werden können. Weiter werden die Typumwandlungen (und die damit verbundenen Fehlerquellen) zwischen den fundamentalen Datentypen besprochen.
Aufgrund der Plattformabhängigkeit der fundamentalen Datentypen in C++ ist es für den Programmierer unerlässlich zu wissen, welcher Datentyp wieviel Speicherplatz belegt und insbesondere in welchen Zahlenbereichen die am häufigsten verwendeten Datentypen (wie short, int, float, double) fehlerfrei eingesetzt werden können.
Da man sich die Grenzen der Zahlenbereiche vermutlich nicht merken kann, sollte man zumindest wissen, wie man sie leicht feststellen kann.
Dazu werden die in Elementare Syntax von C++: Fundamentale Datentypen gestellten Aufgaben gelöst beziehungsweise Lösungshinweise gegeben.
Aufgaben zum Einüben der Arbeitstechniken, die in der strukturierten Programmierung angewendet werden.
Das Wettergeschen kann durch das sochastische Modell einer Markov-Kette simuliert werden. Die Programmieraufgabe beinhaltet, die Eigenschaften einer Markov-Kette zu diskutieren und zu beurteilen, ob das Wettergeschehen damit treffend beschrieben werden kann und wie das Modell durch weiteren Annahmen verbessert werden kann.
Vorgestellt werden mehrere Aufgaben, die als vierwöchige Projektarbeit zu lösen sind. Programmiert werden soll entweder im Sinne der strukturierten Programmierung oder (besser) im Sinne der objekt-orientierten Programmierung.
Die Programmieraufgabe behandelt ein typisches Problem der Datenverarbeitung: Messdaten werden laufend aufgenommen und sollen geeignet ausgewertet werden. Sie können: Erstens direkt angezeigt werden, zweitens sofort in andere relevante Daten umgerechnet und angezeigt werden oder drittens abgespeichert und erst in ihrer Gesamtheit ausgewertet werden. Diese Aufgaben sollen anhand der zu simulierenden Daten, die während einer Fahrradtour anfallen können, eingeübt werden.
Vorgestellt wird ein Problem der Regelungstechnik: Es soll die Umgebung eines Hauses und dessen Heizung simuliert werden. Dabei sollen in konstanten Zeitabständen die Außentemperatur und die Raumtemperatur gemessen werden und ein Algorithmus entwickelt werden, der dafür sorgt, dass die Raumtemperatur der vorgegebenen Soll-Temperatur möglichst nahe kommt.
Matching-Probleme treten dann auf, wenn zwischen zwei Gruppen eine Zuordnung hergestellt werden soll (jedem Bewerber soll eine Stelle vermittelt werden; jedem Gast soll ein Geschenk überreicht werden). Dabei können unterschiedliche Nebenbedingungen hinzutreten (ein Bewerber ist nur für bestimmte Stellen qualifiziert; nicht jedes Geschenk ist für jeden Gast geeignet). Bei kleinen Gruppengrößen können diese Zuordnungen meist direkt gefunden werden; im Allgemeinen versucht man Algorithmen zu formulieren, die die Zuordnungen finden. Matching-Probleme werden in der Graphentheorie behandelt. Die hier vorgestellten Programmieraufgaben sollen einige typische Fragestellungen aufzeigen.
Das Rucksackproblem gehört zur Klasse der Optimierungsprobleme. Dabei sollen aus einer Menge von Gegenständen diejenigen in den Rucksack gepackt werden, die den Wert seines Inhaltes maximieren. Für kleine Anzahlen von Gegenständen kann man die optimale Lösung leicht erraten. Für sehr große Anzahlen kann ein Algorithmus, der alle möglichen Bepackungen durchprobiert, unzumutbare Rechenzeit beanspruchen.
Es wird das Travelling Salesman Problem vorgestellt, für das verschiedene Algorithmen entwickelt werden sollen. Zudem ist eine spezielle Anordnung der Stationen des Handlungsreisenden gegeben, auf die die Algorithmen angewendet werden sollen.
Inhalt und Lernziele des Kapitels Einführung in die Programmierung.
Vorgestellt werden die Design-Prinzipien Komposition und Vererbung, die immer dann eingesetzt werden, wenn Klassen als Datenelemente nicht nur fundamentale Datentypen sondern ihrerseits Klassen enthalten.
Dabei werden weitere anspruchsvolle Konzepte von C++ erläutert: Der Polymorphismus (= Vielgestaltigkeit), Zeiger, das Überschreiben von Funktionen (function overriding) und Operatoren, Implementierung einer Baumstruktur.
Anfangs wurde die Entwicklung von Programmiersprachen als Abfolge von Generationen aufgefasst (binäre Maschinensprache, Assembler, prozedurale Programmiersprache).
Irgendwann wurde dies zu unübersichtlich, so dass man besser von Programmier-Paradigmen spricht, was die unterschiedliche Herangehensweise an ein zu lösendes Problem ausdrücken soll.
Die wichtigsten Paradigmen sind: imperative Programmierung, deklarative Programmierung, funktionale Programmierung, objekt-orientierte Programmierung.
Näher erläutert werden hier die strukturierte Programmierung (als Weiterentwicklung der imperativen Programmierung) und die objekt-orientierte Programmierung.
Es werden die grundlegenden Eigenschaften eines Algorithmus erläutert und der Computer als Maschine vorgestellt, die in der Lage ist, jeden beliebigen Algorithmus abzuarbeiten.
In der Erstellung von Algorithmen konzentriert man sich zunächst auf die Abfolge der Befehle, die in ihrer Gesamtheit das gegebene Problem (meist die Berechnung von Ausgabewerten aus Eingabewerten) lösen. Dabei gerät man schnell zur Frage, wie dabei auftretende veränderliche Größen modelliert werden.
Jede Programmiersprache bietet dazu fundamentale Datentypen an, auf denen gewisse Operationen ausgeführt werden können (wie etwa die ganzen Zahlen zusammen mit den Grundrechenarten).
Vorgestellt werden hier fundamentale Datentypen wie ganze Zahlen, Gleitkommazahlen, logische Werte und Zeichen.
Zu ihrem besseren Verständnis ist es nötig, in Grundzügen die Speicherorganisation kennenzulernen.
Die umgangssprachliche Formulierung eines Algorithmus sollte man nur verwenden, um sich zu übereugen, ob man die Problemstellung verstanden hat. Um die Strukturelemente eines Algorithmus hervorzuheben und damit die Programmierung vorzubereiten, ist eine Formulierung im Pseudocode vorzuziehen. Damit ist man schon näher an einer formalen Sprache, in der eine strenge Syntax eingehalten werden muss und Mehrdeutigkeiten wie in einer natürlichen Sprache nicht vorkommen.
Boolesche Variablen können die beiden Werte TRUE und FALSE annehmen. Sie entstehen zum Beispiel bei Vergleichsoperationen und können durch zahlreiche logische Operationen miteinander verknüpft werden. Insbesondere um Fallunterscheidungen zu formulieren und den Ablauf eines Programmes zu steuern, werden sie eingesetzt.
Um R-Programme schreiben und ausführen zu können, sind einige Vorbereitungen nötig: Installation von R, Installation einer Entwicklungsumgebung, Anlegen und Strukturierung eines Arbeitsverzeichnisses.
Diese Vorbereitungen und kleine erste Programme werden für den Programmier-Einsteiger erläutert.
Weiter werden viele Hinweise gegeben, wie man sich das Arbeiten mit R erleichtern kann.
Die Programmiersprache R besitzt ihr eigenes Konzept, wie die eingebauten Datentypen aufgebaut sind; es unterscheidet sich von vielen anderen Programmiersprachen darin, dass es nicht elementaren Datentypen gibt (wie Zahlen, Zeichen und logische Werte) und zusammengesetzte Datentypen (also zum Beispiel Vektoren von Zahlen). Sondern es gibt nur Vektoren; eine Zahl ist dann ein Spezialfall eines Vektors der Länge 1. Neben den Vektoren gibt es sehr viele weitere vorbereitete Datentypen, so dass man als Programmierer erst für sehr spezielle Anwendungen eigene Datentypen definieren muss. Es wird eine Übersicht über die Datentypen in R gegeben sowie die Vorgehensweise beschrieben, wie man mit ihnen vertraut werden kann.
In R gibt es eigentlich keine elementaren Datentypen (wie Zahlen, logische Werte oder Zeichen), sondern nur Vektoren.
Um die Rechenoperationen (Grundrechenarten, insbesondere Division mit Rest, wissenschaftliche Funktionen) für Zahlen besser kennenzulernen, werden hier Zahlen wie elementare Datentypen behandelt.
Zur Unterscheidung von ganzen Zahlen und Gleitkommazahlen benötigt man die Konzepte Modus und Speicher-Modus.
Es werden erste Beispiele gezeigt, wie man in R mit Variablen umgeht.
Mit den drei Zugriffs-Spezifikationen (access modifier) public, protected und private wird festgelegt, welche Klasse auf welche Datenelemente und Methoden zugreifen kann. Mit ihrer Hilfe lässt sich die Datenkapselung realisieren. Die Zugriffs-Spezifikation ist ein Bestandteil der Deklaration von Datenelementen und Methoden; es wird gezeigt, wie man die Deklarationen einer Klasse übersichtlich in einem UML-Diagramm darstellen kann. UML-Diagramme sind somit eines der wichtigsten Hilfsmittel beim Entwurf komplexer Programme.
Ein Konstruktor legt fest, welche Aktionen beim Erzeugen eines Objektes ausgeführt werden und sind daher ein zentraler Bestandteil einer Klasse. Wie Methoden können sie überladen werden. Die Eigenschaften von Konstruktoren (und des Destruktors, der beim Löschen eines Objektes aufgerufen wird), einige spezielle Konstruktoren (Default-Konstruktor, Kopier-Konstruktor) sowie das Delegations-Prinzip werden hier vorgestellt.
Die zentralen Begriffe zum Verständnis der objekt-orientierten Programmierung sind Klassse und Objekt: Die Klasse ist der allgemeine Bauplan für die konkreten Objekte.
Gezeigt wird die Syntax in C++, mit der Klassen angelegt werden, ihre Datenelemente und Methoden definiert werden, wie konkrete Objekte erzeugt werden und wie diese in anderen Programmen genutzt werden.
Funktionsaufrufe können in C++ entweder mit call by value oder call by reference realisiert werden; beide werden vorgestellt und diskutiert. Rekursionen ermöglichen oft schlanke Quelltexte, die aber schwerer verständlich sind als die entsprechende Implementierung mit Schleifen; einige Beispiele sollen an die Verwendung von Rekursionen heranführen. Die sogenannten Function Templates werden in der C++-Standard-Bibliothek oft eingesetzt; sie sind in einem gewissen Sinn eine Verallgemeinerung des Überladens von Funktionen.
Strukturierte Programmierung heißt vor allem, dass man wiederkehrende Quelltexte zu Unterprogrammen (Funktionen) zusammenfasst.
Dieser Abschnitt zeigt, wie Funktionen in C++ realisiert werden (genauer: wie sie definiert und aufgerufen werden).
Die Quelltexte lassen sich besser strukturieren, wenn man die Definition einer Funktion in Deklaration und Implementierung aufteilt.
Weiter wird das Überladen von Funktionen besprochen.
Um Beispiele zur strukturierten Programmierung zu zeigen, werden einige Funktionen vorgestellt, die mit den Klassen vector und array aus der Standard-Bibliothek arbeiten.
Weiter wird anhand der Beispiele das Konzept des Gültigkeitsbereiches näher erläutert, insbesondere werden Eigenschaften und Einsatz-Möglichkeiten von lokalen Variablen, globalen Variablen und lokalen static-Variablen diskutiert.
Wie im entsprechenden Kapitel zur Einführung in die Programmierung werden hier die kopfgesteuerte Schleife, die fußgesteuerte Schleife und die Schleife mit Zählvariable besprochen und einige Spitzfindigkeiten erklärt, die die C++-Syntax dazu bereithält.
Weiter wird anhand der Schleifen das sehr viel weiter reichende Konzept des Gültigkeitsbereiches (scope) einer Variable vorgestellt.
Die Entwicklungsumgebung Code::Blocks bietet mehrere Möglichkeiten, eine neue Datei oder ein neues Projekt anzulegen; die für den Anfänger relevanten Möglichkeiten werden vorgestellt.
Zudem kann man sehr viel produktiver arbeiten, wenn man die in der Entwicklungsumgebung enthaltenen Helfer kennt (Syntaxhervorhebung, Syntax-Vervollständigung, Code-Refactoring, Code-Schnipsel).
Für die ersten Programme bietet es sich an, Ausgaben und Einagben über die Konsole zu machen.
Die zugehörigen Befehle in C++ werden hier erläutert.
Zugleich werden die Programmbeispiele verwendet, um zahlreiche weiterreichende Konzepte zu erklären:
Präprozessor-Direktive, Kommentare, Namensräume, die besondere Bedeutung der main()-Methode, der Rückgabewert einer Funktion, Quelltextformatierung.
Um C++-Programme schreiben, compilieren und ausführen zu können, muss man sich eine geeignete Umgebung bereitstellen.
Es werden einige Möglichkeiten beschrieben; empfohlen wird die Entwicklungsumgebungen Code::Blocks, die es in einer Version mit integriertem MinGW-Compiler gibt.
Inhaltsverzeichnis und Lernziele des Kapitels C++: Fortgeschrittene Syntax.
Inhalt und Lernziele des Kapitels Einführung in C++.
Einige einfache arithmetische Operationen können in C++ in einer Kurzform geschrieben werden (Inkrement-Operator, Dekrement-Operator, Kurzform-Operatoren).
Wenn möglich sollen diese auch eingesetzt werden, da sie schneller ausgeführt werden als die entsprechenden Befehle in der ausführlichen Schreibweise.
Die Aufgaben des Betriebssystems werden genannt und Prozess-Management und Speichermanagement näher erläutert.
Außer den allseits bekannten Notebooks und PCs gibt es eine Vielzahl von Computersystemen mit unterschiedlicher Leistungsfähigkeit in vielfältigen Anwendungsgebieten.
Die wichtigsten dieser Computersysteme werden hier kurz vorgestellt.
Je nach Betriebsart eines Computers muss ein anderes Betriebssystems ausgewählt werden.
Unter einer Betriebsart eines Computers versteht man eine Auswahl aus den 4 Alternativen:
Single–Processor–/Multiprocessor–System, Single–Tasking–/Multitasking–System, Single–User–/Multiuser–System, Batch–/Dialog–System.
Inhalt und Lernziele des Kapitels Rechnerarchitektur.
Aufgaben zum Selbststudium.
Inhalt der Aufgaben ist das Kapitel Einführung in die Programmierung.
Einführung in die Informatik für Ingenieure und Naturwissenschaftler. Kurs zum Selbststudium, der das Grundwissen in Informatik etwa im Umfang einer einsemestrigen Vorlesung zusammenstellt.
Als Strukturelemente von Algorithmen werden diejenigen Muster bezeichnet, nach denen die Befehle eines Algorithmus verknüpft werden können. Hier werden die Strukturelemente zunächst allgemein vorgestellt; später werden Beispiele im Pseudocode und in speziellen Programmiersprachen angegeben.
Der bisher etwas saloppe Begriff eines Algorithmus wird hier präzisiert. Ferner werden einige mit dem Algorithmus verwandte Begriffe erläutert.