Eine Zufallsvariable ist ein zentrales Konzept in der Wahrscheinlichkeitstheorie. Sie ist eine mathematische Funktion, die jedem Ergebnis eines Zufallsexperiments einen numerischen Wert zuordnet.
Zufallsvariablen können diskret oder stetig sein. Diskrete Zufallsvariablen nehmen nur bestimmte Werte an, während stetige Zufallsvariablen jeden Wert innerhalb eines bestimmten Intervalls annehmen können. Beispiele für diskrete Zufallsvariablen sind die Anzahl der Würfe beim Werfen eines Würfels oder die Anzahl der Kunden, die einen Laden betreten. Stetige Zufallsvariablen hingegen können beispielsweise die Größe oder das Gewicht von Objekten beschreiben.
Die Eigenschaften von Zufallsvariablen können mithilfe von verschiedenen statistischen Maßen quantifiziert werden. Der Erwartungswert gibt den durchschnittlichen Wert einer Zufallsvariable an, während die Varianz und die Standardabweichung die Streuung um den Erwartungswert messen. Quantile und Median geben Auskunft über die Verteilung der Zufallsvariable.
Die Zufallsvariable spielt auch eine wichtige Rolle bei der Modellierung und Analyse von komplexen Systemen. Ein Beispiel dafür ist der mehrarmige Bandit, ein mathematisches Modell für Entscheidungsprobleme mit unsicherer Belohnung. Hierbei werden verschiedene Handlungsoptionen (Arme) ausprobiert, um die beste Belohnung zu finden. Die Zufallsvariable wird verwendet, um die zu modellieren und Algorithmen zur Entscheidungsfindung zu entwickeln.
In unserem umfangreichen Artikelarchiv haben wir bereits viele Artikel zu diesem Thema verfasst. Dazu gehören Definitionen und Beispiele zur Entropie, zur Tschebyscheff-Ungleichung und zur Berechnung von Erwartungswerten und Varianzen. Außerdem behandeln wir spezielle Wahrscheinlichkeitsverteilungen wie die geometrische und die hypergeometrische Verteilung.
An einfachen Beispielen wird gezeigt, welche Eigenschaften verwendet werden, um eine Markov-Kette zu definieren. Sie stellt eine Verallgemeinerung der unabhängigen Zufallsvariablen dar. Und zwar in dem Sinn, dass in einer Folge von Zufallsvariablen jede Zufallsvariable nur vom Wert der vorhergehenden, nicht aber von noch weiter zurückliegenden Zufallsvariablen abhängt. Die zentrale mathematische Größe zur Beschreibung einer Markov-Kette ist die Übergangsmatrix, welche die Übergangswahrscheinlichkeiten zwischen den möglichen Zuständen (Werten der Zufallsvariablen) festlegt.
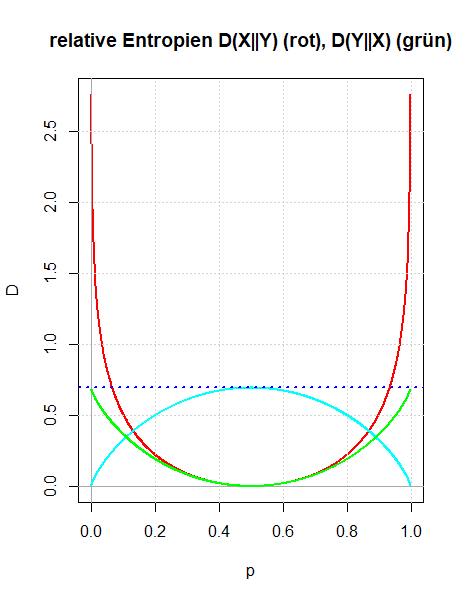
Es werden zwei Zugänge gezeigt, wie man die relative Entropie motivieren kann: Entweder als Verallgemeinerung der gegenseitigen Information oder indem man die Überlegungen Boltzmanns zur Definition der Entropie in dem Sinn verallgemeinert, dass man die Voraussetzung der Gleichwahrscheinlichkeit der Mikrozustände aufgibt. Die Bedeutung der relativen Entropie als einer Größe, die quantifiziert, wie unterschiedlich zwei Wahrscheinlichkeitsverteilungen sind, wird durch den zweiten Zugang besser verständlich.
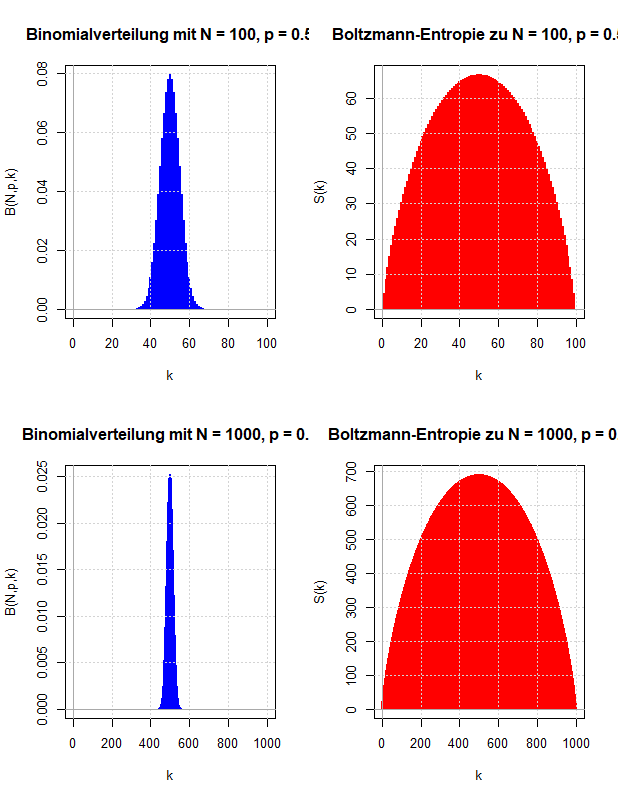
Ludwig Boltzmann gab eine mikroskopische Erklärung für die thermodynamische Entropie, die nach dem zweiten Hauptsatz der Thermodynamik niemals abnehmen kann. Diese Überlegungen werden verwendet, um zu motivieren, wie die Entropie der Wahrscheinlichkeitstheorie definiert wird, die die Ungewissheit über den Wert einer Zufallsvariable quantifizieren soll.
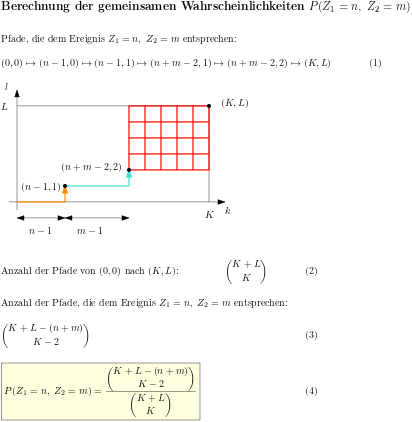
Die Entropie einer Zufallsvariable, die gemeinsame Entropie zweier Zufallsvariablen und die gegenseitige Information werden am Beispiel der Wartezeitprobleme beim Ziehen ohne Zurücklegen veranschaulicht. Dazu werden als Zufallsvariablen die Wartezeit bis zum ersten Treffer und die Wartezeit vom ersten bis zum zweiten Treffer verwendet.
Überträgt man den Begriff der Entropie einer Zufallsvariable auf die Wahrscheinlichkeitsverteilungen von zwei Zufallsvariablen, so ist es naheliegend die gemeinsame Entropie und die bedingte Entropie einzuführen, die über die Kettenregel miteinander verknüpft sind. Diese wiederum motiviert die Einführung einer neuen Größe, der gegenseitigen Information zweier Zufallsvariablen. Sie ist symmetrisch in den beiden Zufallsvariablen und beschreibt die Information, die in einer Zufallsvariable über die andere Zufallsvariable enthalten ist. An einfachen Beispielen wird die Definition der gegenseitigen Information motiviert und veranschaulicht.
Die Entropie wurde eingeführt als ein Maß für die Ungewissheit über den Ausgang eines Zufallsexperimentes. Entsprechend kann man eine bedingte Entropie definieren, wenn man die bedingten Wahrscheinlichkeiten verwendet, wobei man als Bedingung entweder ein Ereignis oder eine Zufallsvariable zulässt. Die Definition der bedingten Entropie und ihr Zusammenhang mit der gemeinsamen Entropie zweier Zufallsvariablen (Kettenregel) wird an einfachen Beispielen erläutert.
Akzeptiert man die Entropie als eine Kenngröße einer Wahrscheinlichkeitsverteilung, die die Ungewissheit über den Ausgang eines Zufallsexperimentes beschreibt, so wird man fordern, dass sich bei unabhängigen Zufallsexperimenten die Entropien addieren.
Um diese Aussage schärfer formulieren zu können, wird die gemeinsame Entropie H(X, Y) von zwei Zufallsvariablen eingeführt.
Es wird gezeigt, dass die übliche Definition der Entropie die Additivitätseigenschaft bei unabhängigen Zufallsvariablen X und Y besitzt.
Die geometrische Verteilung kann als Verteilung von Wartezeiten aufgefasst werden, wenn man einen Münzwurf solange wiederholt bis der erste Treffer eintritt: man berechnet die Wahrscheinlichkeiten der Anzahl der nötigen Würfe. Man kann dieses Wartezeitproblem verallgemeinern, indem man nicht bis zum ersten sondern bis zum r-ten Treffer wartet. Die Verteilung dieser Wartezeiten wird berechnet und die Eigenschaften der dabei entstehenden Verteilung wird untersucht.
Die Jensensche Ungleichung liefert eine Abschätzung zwischen der Anwendung einer Funktion auf eine konvexe Kombination beziehungsweise der konvexen Kombination der Funktionswerte. Je nachdem, ob die Funktion konvex oder konkav ist, erhält man ein anderes Ungleichheitszeichen zwischen den genannten Termen. Im Folgenden werden die zum Beweis der Jensenschen Ungleichung nötigen Eigenschaften von konvexen Funktionen erläutert, die Jensensche Ungleichung formuliert und bewiesen und einige Anwendungen gezeigt (Ungleichung zwischen dem geometrischen und dem arithmetischen Mittel, Anwendung der Jensenschen Ungleichung auf Erwartungswerte von Zufallsvariablen).
Die Definition der Entropie eines Wahrscheinlichkeitsmaßes oder einer Zufallsvariable wird an einfachen Beispielen erläutert. Es wird diskutiert, dass die Entropie kein Streuungsmaß ist (wie die Standardabweichung), sondern die Ungewissheit (oder Unbestimmtheit) des Ausgangs eines Zufallsexperimentes beschreibt.
Die Methode, den Erwartungswert einer Zufallsvariable X mit Hilfe von Indikatorvariablen zu berechnen, ist deshalb so wichtig, weil man dazu die Verteilung von X nicht kennen muss. Die eigentliche Schwierigkeit besteht oft darin, geeignete Indikatorvariablen zu finden. An mehreren Beispielen (Münzwurf, hypergeometrische Verteilung und einer Zufallsvariable mit unbekannter Verteilung) wird dieses Vorgehen demonstriert. Da man Varianzen auf Erwartungswerte zurückführen kann, lassen sich mit dieser Methode auch Varianzen und Standardabweichungen berechnen.
Die hypergeometrische Verteilung beschreibt die Wahrscheinlichkeit dafür, dass beim Ziehen ohne Zurücklegen n Treffer aus einer Urne gezogen werden; dazu befinden sich in der Urne anfangs L Treffer und K Nieten und es werden N Lose entnommen. Die Abhängigkeit der Verteilung von den drei Parametern K, L und N erschwert den Zugang zur Berechnung der gesuchten Wahrscheinlichkeiten. Es werden zwei - natürlich gleichwertige - Methoden gezeigt, wie man die Wahrscheinlichkeiten berechnet.
Das p-Quantil als Umkehrfunktion der Verteilungsfunktion und der Spezialfall des Medians als p-Quantil zur Wahrscheinlichkeit p = 0.5 werden vorgestellt.
Die geometrische Verteilung wird verwendet, um Wartezeiten zu modellieren. Die grundlegenden Eigenschaften wie Erwartungswert, Varianz, Standardabweichung, die Verteilungsfunktion und insbesondere der Zusammenhang zur Binomialverteilung und die sogenannte Gedächtnislosigkeit werden besprochen.
Die Funktion sample() wird verwendet, um Stichproben zu erzeugen. Sie lässt sich so konfigurieren, dass man die Wahrscheinlichkeitsverteilungen von beliebigen selbstdefinierten diskreten Zufallsvariablen einsetzen kann. Zudem kann man das Ziehen mit beziehungsweise ohne Zurücklegen realisieren.
Die Faltung von Wahrscheinlichkeitsmaßen ist eine der wichtigsten Begriffsbildungen, um Summen von unabhängigen Zufallsvariablen zu beschreiben, da sich mit ihr viele Eigenschaften von Zufallsvariablen und Wahrscheinlichkeitsverteilungen prägnant formulieren lassen und zahlreiche Bezüge zu anderen (scheinbar entfernten) Begriffen und Aussagen herstellen lassen. In diesem einführenden Kapitel wird auf exakte mathematische Definitionen und Beweise verzichtet, stattdessen soll der Begriff der Faltung an typischen Beispielen motiviert werden.
Nach dem Erwartungswert sind die Varianz und die Standardabweichung (als Wurzel der Varianz) die wichtigsten Kennzahlen einer Verteilung. Ist der Erwartungswert ein Maß für die Lage der Verteilung, beschreiben Varianz und Standardabweichung die Streuung der Werte einer Zufallsvariable um den Erwartungswert. Die Definition und Eigenschaften werden besprochen und an zahlreichen Beispielen erläutert.
Der Erwartungswert einer Zufallsvariable ist die wichtigste Kennzahl, um Ergebnisse von Zufallsexperimenten zu beschreiben. Seine Definition und Eigenschaften werden ausführlich erläutert. An zahlreichen Beispielen wird seine Berechnung vorgeführt; dabei werden nebenbei wichtige Wahrscheinlichkeits-Verteilungen vorgestellt.
Die Herleitung der Chernoff-Schranke beruht auf der momentenerzeugenden Funktion. Für den Spezialfall der Binomialverteilung kann die optimale Chernoff-Schranke explizit berechnet werden und es geht außer der Markov-Ungleichung keine weitere Näherung ein. Um die Vorgehensweise bei der Berechnung der Chernoff-Schranke besser verständlich zu machen, werden alle Herleitungsschritte besprochen und mit zahlreichen Diagrammen veranschaulicht.
Zu den wichtigsten Wahrscheinlichkeitsverteilungen gibt es Funktionen zum Berechnen der Wahrscheinlichkeitsdichte, der Verteilungsfunktion, des p-Quantils und zum Erzeugen von Zufallszahlen. Für ausgewählte Verteilungen (Binomialverteilung, Poisson-Verteilung, kontinuierliche Gleichverteilung und Normalverteilung) werden diese Funktionen vorgestellt. Dabei werden typische Anwendungen aus der Wahrscheinlichkeitsrechnung und Statistik gezeigt, die zugleich einige Eigenschaften dieser Verteilungen illustrieren.
Zufallsvariablen können diskrete oder kontinuierliche Werte annehmen. Die mathematische Beschreibung unterscheidet sich, da die Wahrscheinlichkeiten der Werte der Zufallsvariable entweder mit Folgen oder indirekt über eine Wahrscheinlichkeitsdichte angegeben werden. Diese Beschreibung wird an speziellen Verteilungen demonstriert: diskrete Gleichverteilung, Poisson-Verteilung, kontinuierliche Gleichverteilung, Standard-Normalverteilung.
Die Tschebyscheff-Ungleichung als einfachste Konzentrations-Ungleichung wird aus mehreren Perspektiven beleuchtet: Es werden Beispiele für ihre typische Anwendung besprochen; es wird ein direkter Beweis gegeben; es wird gezeigt, dass sie als Spezialfall der verallgemeinerten Markov-Ungleichung aufgefasst werden kann; es wird diskutiert, wie gut die Abschätzung ist, die sie liefert. In den R-Skripten werden die Berechnungen aus den Anwendungsbeispielen ausgeführt, die man ohne Programmierung kaum bewältigen könnte.
Zufallsvariablen sind die geeignete Begriffsbildung um sowohl Ereignisse als auch deren Wahrscheinlichkeiten treffend zu beschreiben und zu berechnen. In späteren Anwendungen der Wahrscheinlichkeitsrechnung werden Zufallsvariablen ständig eingesetzt. Hier wird zunächst gezeigt, wie Zufallsvariablen mit der Ereignisalgebra und dem Wahrscheinlichkeitsmaß zusammenhängen und sich so nahtlos in den Aufbau der Wahrscheinlichkeitsrechnung einfügen. In den R-Skripten wird gezeigt, wie man Zufallsvariable leicht modellieren kann.
Ein Algorithmus zur Simulation von N Spielen am k-armigen Banditen (multi-armed bandit) wird in R implementiert. Der Algorithmus erlaubt die Auswahl einer Strategie zur Wahl des nächsten zu spielenden Armes. Als Strategien stehen die im Artikel "Der mehrarmige Bandit (multi-armed bandit): Simulationen mit einfachen Algorithmen vorgestellten Strategien zur Auswahl, es können aber leicht weitere Strategien implementiert und eingefügt werden.
Um beim Spiel am mehrarmigen Banditen einen möglichst hohen Gewinn zu erzielen, benötigt man eine Strategie, die einen Kompromiss zwischen Exploration und Exploitation herstellt. Es werden einfache Algorithmen vorgestellt, die dieses Problem lösen und ihre Eigenschaften werden mit Hilfe von Simulationen untersucht.
Beim mehrarmigen Banditen oder genauer k-armigen Banditen kann man ein Glücksspiel durch Betätigen eines Armes auslösen. Mathematisch modelliert werden sie durch Zufallsvariablen mit unterschiedlichen Erwartungswerten. Möchte man am k-armigen Banditen N Spiele durchführen und dabei einen möglichst hohen Gewinn erzielen, gerät man in ein Dilemma: Einerseits muss man alle Arme untersuchen, um ihre Kennzahlen zu schätzen (Exploration), andererseits möchte man möglichst oft den besten Arm betätigen (Exploitation). Im nächsten Kapitel werden dann Algorithmen entwickelt, die versuchen einen Kompromiss zwischen Exploration und Exploitation herzustellen.