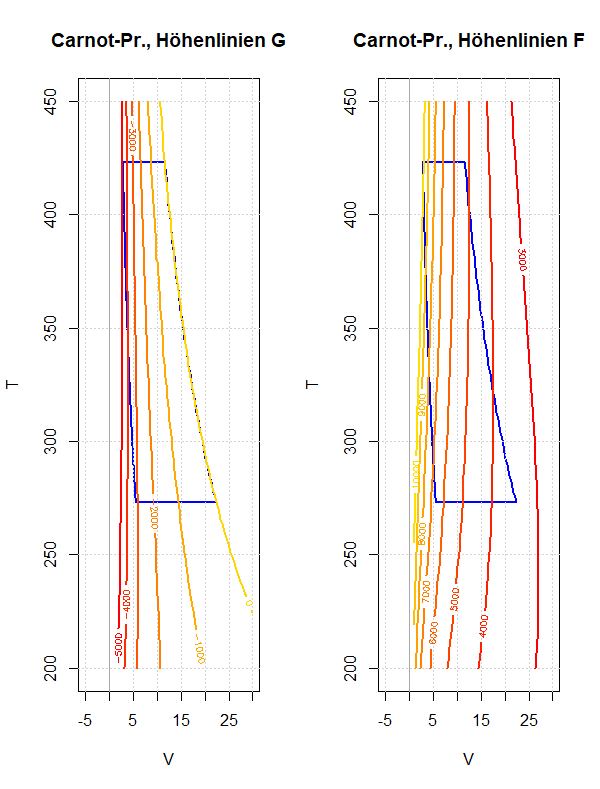
Am Beispiel des Carnot-Prozesses soll das Verhalten der freien und der gebundenen Energie während eines Umlaufs diskutiert werden. Dies soll die Bedeutung dieser thermodynamischen Potentiale besser verständlich machen; speziell ob und wie sie als Arbeitsfähigkeit beziehungsweise Wärmeinhalt eines Systems interpretiert werden können.
Am Beispiel der isochoren Erwärmung werden die Eigenschaften der freien Energie F = U - TS und der gebundenen Energie G = TS erläutert. Speziell wird gezeigt, wie man ihre Veränderung darstellen kann, wenn man vom US-Diagramm zum TS-Diagramm übergeht.
Die freie Energie F = U - TS ist die (negative) Legendre-Transformierte der inneren Energie U, wenn diese als Funktion der extensiven Variablen Entropie S und Volumen V dargestellt wird: U = U(S, V); die Legendre-Transformation wird dabei bezüglich der Variable S berechnet. Es ist dann leicht nachzuweisen, dass die freie Energie ein thermodynamisches Potential ist und dass die Änderung der freien Energie bei isothermen Zustandsänderungen mit der Zufuhr von mechanischer Arbeit übereinstimmt.
Mit Hilfe der freien Energie und der gebundenen Energie soll die innere Energie in zwei Anteile zerlegt werden: Die freie Energie soll allein durch die Zufuhr von mechanischer Arbeit und die gebundene Energie allein durch die Zufuhr von Wärme verändert werden. Diese Zerlegung lässt sich allerdings nur für isotherme Prozesse durchführen. Die Eigenschaften der freien und gebundenen Energie werden für die isotherme Zustandsänderung und andere einfache Prozesse diskutiert.
Mit dem Druckausgleich (also zwei Kammern mit einer beweglichen Trennwand, in der sich anfangs Gase mit unterschiedlichem Druck befinden) lassen sich zahlreiche Aspekte der Entropie und allgemeiner der Thermodynamik demonstrieren (reversible und irreversible Prozessführung, Eindeutigkeit des Endzustandes, Maximum der Entropie, Temperatur- und Volumenabhängigkeit der Entropie).
Wird die innere Energie als Funktion der extensiven Variablen dargestellt, enthält sie sämtliche Eigenschaften des entsprechenden thermodynamischen Systems; dies rechtfertigt die innere Energie als thermodynamisches Potential zu bezeichnen. Untersucht man speziell die innere Energie bei adiabatischen Zustandsänderungen, so kann man leicht motivieren, weshalb andere thermodynamische Potentiale (wie freie Energie oder Enthalpie) eingeführt werden. Am idealen einatomigen Gas werden diese Eigenschaften der inneren Energie demonstriert.
Der Carnot-Prozess ist sowohl inhaltlich als auch methodisch wichtig für die Thermodynamik: Seine Analyse liefert zahlreiche Einsichten in ihre Konzepte, Argumentationsweisen und technische Anwendungen.
Für das ideale einatomige Gas werden die Zusammenhänge zwischen den Hauptsätzen der Thermodynamik und den Zustandsgleichungen (thermische und kalorische Zustandsgleichung) diskutiert und angewendet, um die Entropie in verschiedenen Darstellungen zu berechnen. Illustriert werden die Herleitungen an speziellen Zustandsänderungen (isotherm, isochor, adiabatisch, freie Expansion).
In den vorausgegangenen Kapiteln wurden die Abzählprobleme behandelt, die sich ergeben, wenn ein thermodynamisches System entweder auf der Ebene der Mikrozustände oder der Makrozustände beschrieben wird. Vergleicht man diese Ergebnisse mit den Gleichungen der phänomenologischen Thermodynamik, kann man eine statistische Definition der Entropie ableiten und damit eine (statistische) Erklärung des zweiten Hauptsatzes der Thermodynamik liefern. Die Boltzmann-Entropie wird mit Hilfe der Anzahl der Mikrozustände pro Makrozustand definiert und besitzt die Eigenschaften, die man innerhalb der Thermodynamik an die Entropie stellt.