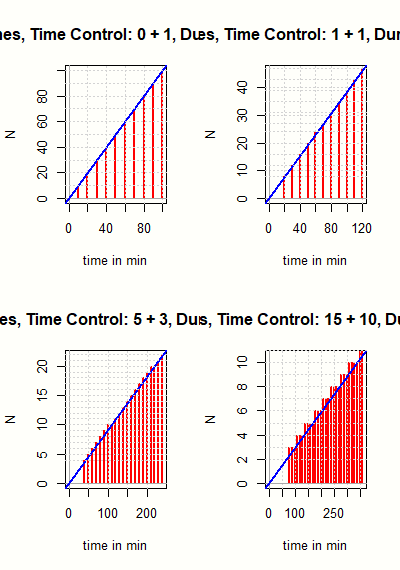
Es wird ein Turniermodus vorgeschlagen und beschrieben, der die meisten Vorteile der bisherigen Arena-Turniere auf Lichess besitzt. Die Anzahl der Partien pro Turnier ist beschränkt und die möglichen Zeitkontrollen ergeben sich aus der Fibonacci-Folge. Die bisherigen Arena-Turniere bevorzugen Spieler, die schneller spielen als nach der eigentlich vorgesehenen Zeitkontrolle. Die Fibonacci-Arena soll dagegen einen Anreiz liefern, die Bedenkzeit voll auszunutzen und wird daher einen anderen Spielerkreis ansprechen. Diskutiert werden die Vor- und Nachteile der Turniertypen und es werden Hinweise zur Durchführung der Fibonacci-Arena gegeben.
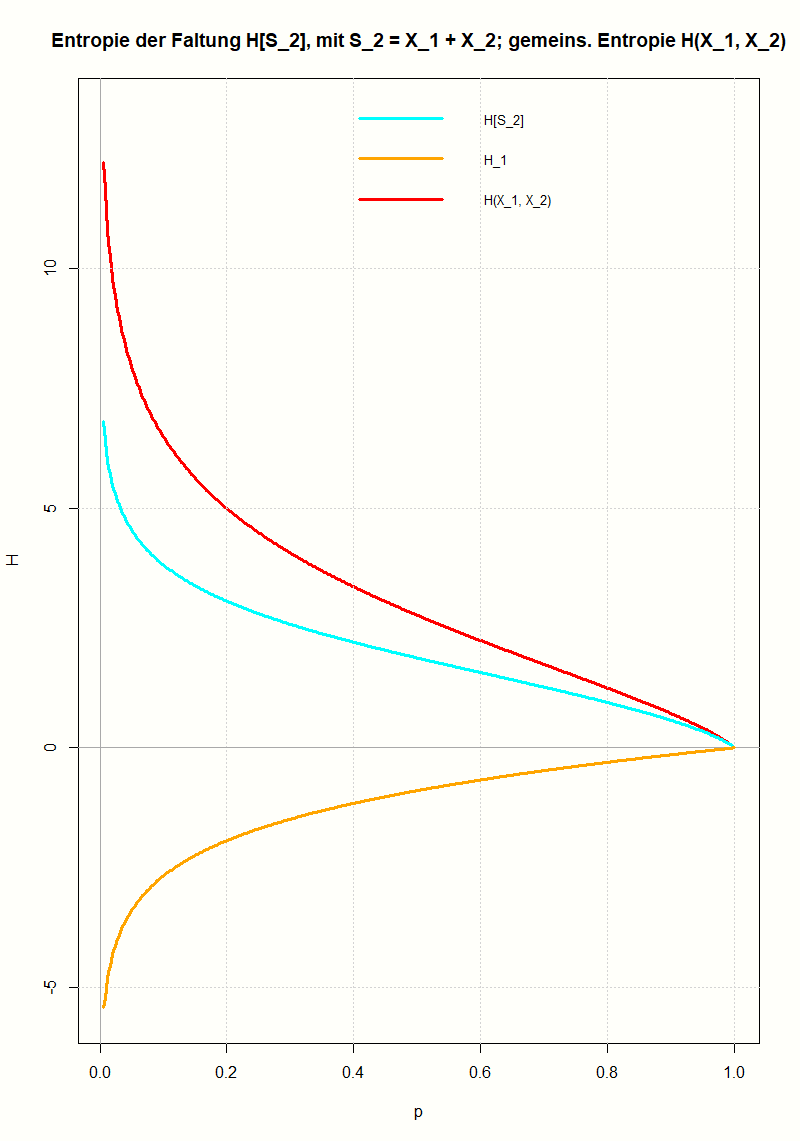
Am Beispiel der geometrischen Verteilung wird gezeigt, wie man die Entropie einer Faltung berechnet und wie sie mit den Entropien der Ausgangsverteilungen zusammenhängt. Mit Hilfe der Log-Summen-Ungleichung (einer Folgerung aus der Jensenschen Ungleichung) lässt sich das Ergebnis für beliebige Verteilungen verallgemeinern.
Bitweise Operatoren gehören zu den unterschätzten Werkzeugen in der Programmierung. Wer sie beherrscht, kann Daten kompakter speichern, Informationen blitzschnell verarbeiten und sogar clevere Tricks auf Byte-Ebene anwenden.
In diesem Artikel schauen wir uns an, wie man Daten effizient packt und entpackt, Farbkanäle aus RGB-Werten extrahiert, Flags mit Bitmasken verwaltet – und ganz nebenbei, wie man mit wenigen Zeilen Code Groß- und Kleinschreibung umwandeln kann.
An einfachen Beispielen wird gezeigt, welche Eigenschaften verwendet werden, um eine Markov-Kette zu definieren. Sie stellt eine Verallgemeinerung der unabhängigen Zufallsvariablen dar. Und zwar in dem Sinn, dass in einer Folge von Zufallsvariablen jede Zufallsvariable nur vom Wert der vorhergehenden, nicht aber von noch weiter zurückliegenden Zufallsvariablen abhängt. Die zentrale mathematische Größe zur Beschreibung einer Markov-Kette ist die Übergangsmatrix, welche die Übergangswahrscheinlichkeiten zwischen den möglichen Zuständen (Werten der Zufallsvariablen) festlegt.
Das DRY-Prinzip ("Don't Repeat Yourself") gehört zu den Grundpfeilern wartbarer Softwarearchitektur. In der Praxis wird dieses Prinzip jedoch häufig durchbrochen – insbesondere beim Einsatz von Spring Data Repositories. Wiederkehrende Datenzugriffslogik wie findByStatus oder markAsProcessed taucht oft mehrfach auf, nur leicht variiert für unterschiedliche Entitäten. Ein typisches Beispiel dafür bietet die Implementierung des Outbox-Patterns. Solche Wiederholungen führen schnell zu redundanter, schwer wartbarer Codebasis. Dieser Artikel zeigt, wie sich durch den gezielten Einsatz von @NoRepositoryBean und Spring Expression Language (SpEL) wiederverwendbare Repository-Verträge realisieren lassen – elegant, robust und ganz im Sinne von DRY.
Ist es wirklich ein Hack, wenn man eine Website auf PHP 5.6 zum Absturz bringt? Eigentlich ist das Gegenteil die Kunst: Sie überhaupt noch am Laufen zu halten. 4chan bewies mal wieder: Wer 2025 auf Digital-Archäologie setzt, braucht sich über Einbrüche nicht zu wundern.
Wer sich ernsthaft mit digitaler Privatsphäre beschäftigt, bewegt sich wie in einem endlosen Spin-off – voller Nebenhandlungen, Halbwahrheiten und paranoider Plot-Twists.
Ein Internet-Meme bringt es treffend auf den Punkt und illustriert auf herrlich absurde Weise die Eskalationsstufen des Datenschutzfanatismus:
Kommt mit uns auf eine skurrile, aber aufschlussreiche Reise durch die „Stufen der digitalen Paranoia“, wo datenschutzbewusste Nutzer von ahnungslosen Windows-Noobs zu Off-Grid Digital-Eremiten mutieren.
In einer bizarren, aber brillanten Wendung der Geschichte nutzte der Reddit-Nutzer Sourcecode12 eine kleine Armee von KI-Werkzeugen,
um ein urkomisches alternatives Ende für den Zweiten Weltkrieg zu erschaffen – eines, bei dem der Konflikt abrupt nicht durch Diplomatie, sondern durch interstellare Zootierpfleger beendet wird, die genug von den gewalttätigen Eskapaden der Menschheit haben.
Von Smartphones bis Kampfjets, Windturbinen bis zu KI-Chips, seltene Erden (REEs - Rare Earth Elements) sind die stillen Helden des 21. Jahrhunderts. Diese 17 Metallelemente, bestehend aus den 15 Lanthanoiden sowie Scandium und Yttrium, besitzen einzigartige magnetische, lumineszierende und elektrochemische Eigenschaften, die sie in fortgeschrittenen Technologien unersetzlich machen.
Trotz ihres irreführenden Namens sind REEs in der Erdkruste nicht wirklich selten. Die eigentliche Herausforderung liegt in ihrer geologischen Verteilung und den Umweltkosten der Gewinnung und Verarbeitung, was wirtschaftlich rentable Quellen limitiert und die geopolitische Kontrolle weiter konzentriert.
Lerne, wie du mit HTML, CSS und JavaScript ein einfaches Tic-Tac-Toe-Spiel erstellst. Dieses Tutorial führt dich Schritt für Schritt durch die Spiellogik, das Event-Handling mit JavaScript und den Aufbau des HTML-Templates.
In Java werden Enums in Datenbanken typischerweise entweder durch ihre ordinalen Werte oder ihre Namen (Strings) gespeichert.
Dieser Ansatz ist zwar einfach, aber nicht immer ideal. Enum-Namen sind direkt an den Anwendungscode gebunden und können sich ändern, während ordinale Werte noch problematischer sind – eine Änderung der Enum-Reihenfolge kann die Datenkonsistenz gefährden.
Ein flexiblerer und datenbankfreundlicherer Ansatz ist erforderlich, insbesondere wenn man mit Konstanten arbeitet,
die nicht den Java-Enum-Konventionen entsprechen, oder wenn man die Datenbankstruktur von der internen Anwendungslogik entkoppeln möchte.
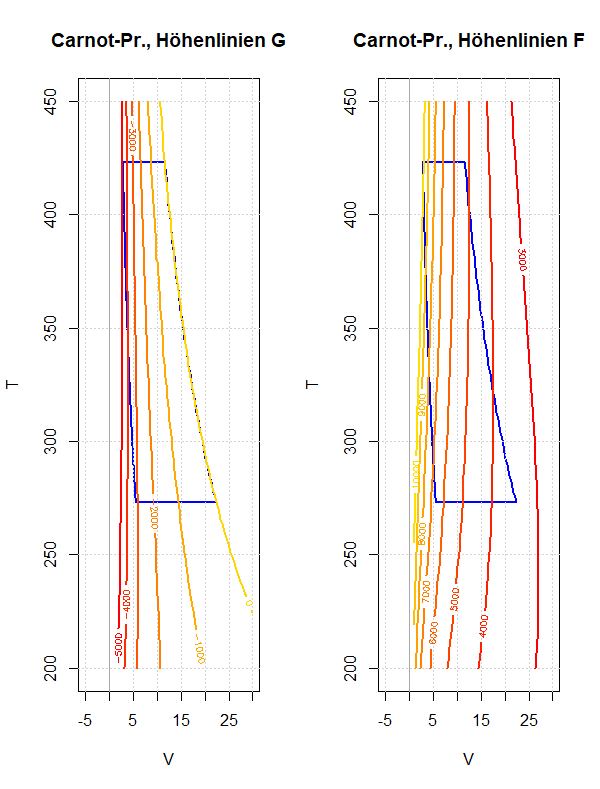
Am Beispiel des Carnot-Prozesses soll das Verhalten der freien und der gebundenen Energie während eines Umlaufs diskutiert werden. Dies soll die Bedeutung dieser thermodynamischen Potentiale besser verständlich machen; speziell ob und wie sie als Arbeitsfähigkeit beziehungsweise Wärmeinhalt eines Systems interpretiert werden können.
Ein raffinierter Phishing-Angriff, der gezielt Google-Konten ins Visier nimmt, wurde aufgedeckt. Die Angreifer machten sich dabei den offiziellen URL-Shortcut von Google, g.co, zunutze, um ihre Opfer zu täuschen.
Besonders bemerkenswert ist, dass dieser Angriff selbst technisch versierte Nutzer beinahe überlistete.
Mit einem vielschichtigen Ansatz gelang es den Tätern, das Vertrauen in die Marke und Infrastruktur von Google gezielt zu missbrauchen.
Kürzlich teilte ein junger Hacker, bekannt als "Daniel", detaillierte Informationen über einen vermeintlichen "Deanonymisierung Angriff" auf Cloudflare – ein bekanntes Content Delivery Network (CDN) – und stellte Fragen zur Sicherheit der Nutzer und zum Datenschutz auf.
Python-Listen sind eine der zentralen Datenstrukturen in der Programmiersprache Python.
Sie ermöglichen das Speichern und Organisieren unterschiedlichster Datentypen, darunter Zahlen, Zeichenketten und komplexe Objekte.
Mit ihrer einfachen Syntax und den zahlreichen integrierten Funktionen bieten Listen vielseitige Werkzeuge zur Datenverarbeitung.
Dieser Artikel behandelt die Grundlagen der Arbeit mit Listen, einschließlich ihrer Erstellung und der Zugriffsmöglichkeiten,
und geht anschließend auf fortgeschrittene Techniken wie das Slicen und Kombinieren von Listen ein.
Mit dem Aufstieg von künstlicher Intelligenz und Automatisierung überdenken Unternehmen,
wie sie die neuen Entwicklungen in existierende Geschäftsprozesse integrieren.
Inmitten dieser Transformation hat ein Startup entschieden, einen radikalen Schritt nach vorne zu machen: Artisan.
Tuples gehören in Python zu den wichtigsten Datenstrukturen und finden überall Anwendung, von kleinen bis zu sehr komplexen Projekten.
Sie dienen dazu, mehrere Werte in einer einzigen Variablen zu gruppieren, ähnlich wie Listen.
In diesem Artikel werden wir uns eingehend mit der Syntax, den grundlegenden Funktionen und Operationen
sowie den Einsatzmöglichkeiten von Tupeln beschäftigen.
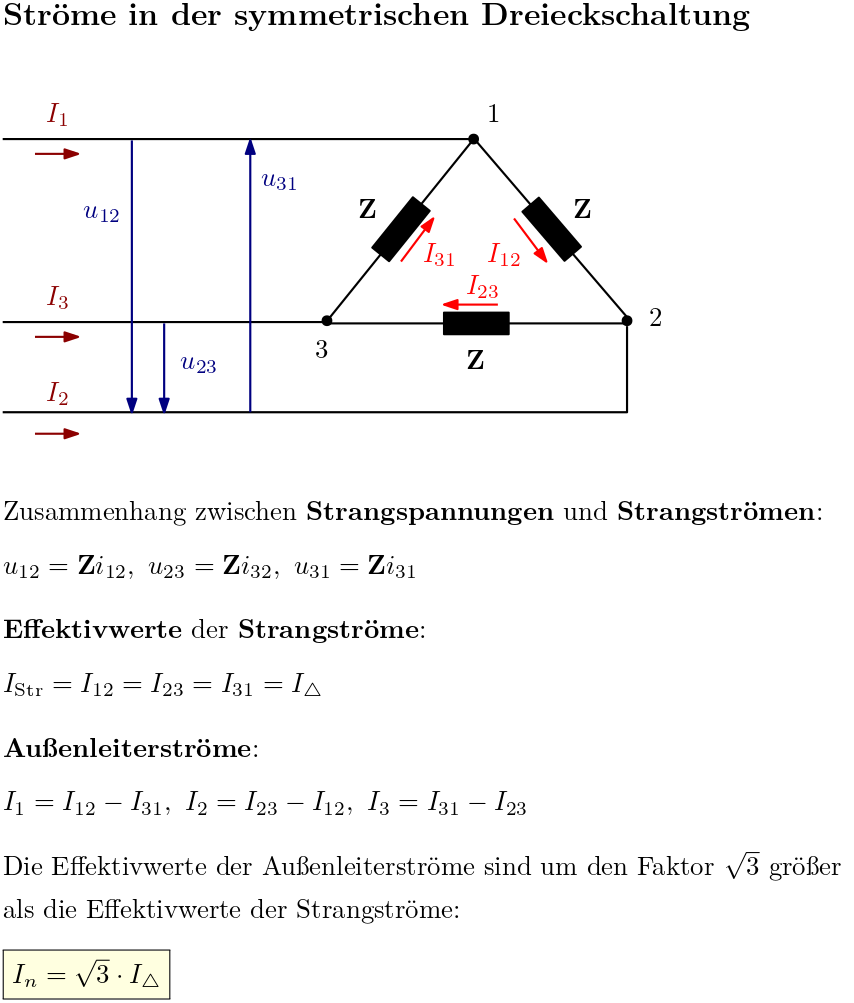
Werden die Verbraucher eines Mehrphasensystems zu einem Ring verkettet, so spricht man im Fall des Dreiphasensystems von der Dreieckschaltung. Diskutiert werden der Aufbau der symmetrischen Dreieckschaltung, die Zusammenhänge zwischen Außenleiterspannung und Strangspannung beziehungsweise Außenleiterstrom und Strangstrom sowie die Berechnung der Leistungen (Wirkleistung, Blindleistung, Scheinleistung).
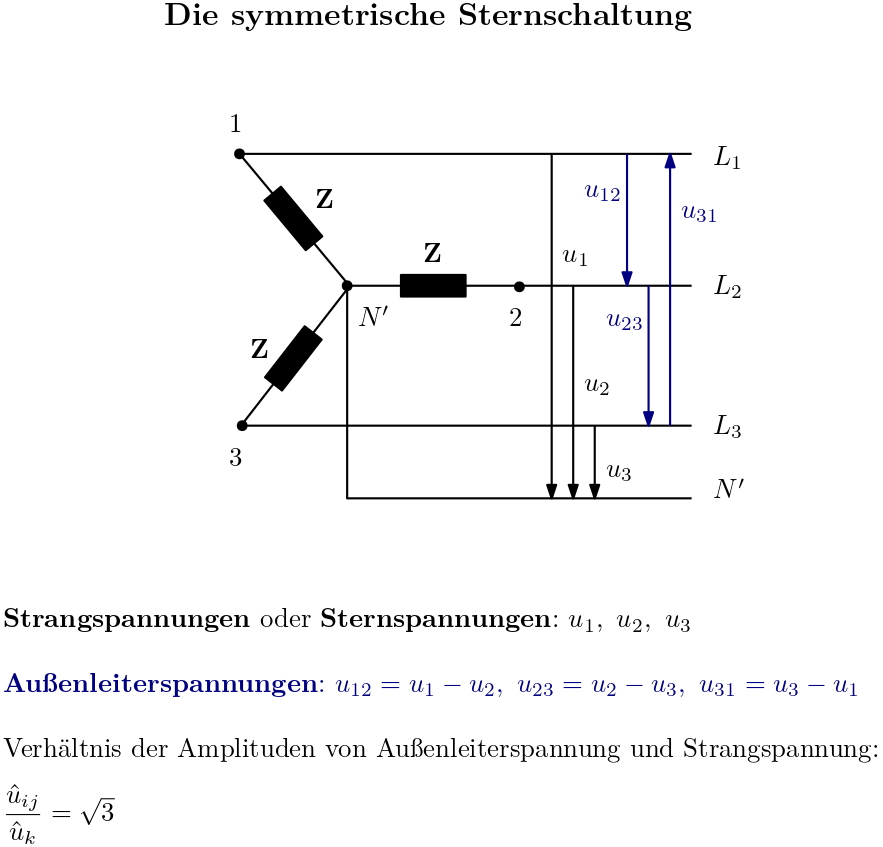
Ein Generator mit gegeneinander verdrehten Wicklungen erzeugt phasenverschobene Spannungen. Diese Spannungen können auf verschiedene Arten eingesetzt werden, um Verbraucher zu versorgen. Eine Möglichkeit besteht darin, sowohl die Spannungsquellen als auch die Verbraucher zu verketten und sie in je einem Sternpunkt zusammenzuführen; die beiden Sternpunkte werden dann leitend miteinander verbunden. Es entsteht die Sternschaltung, die in der Technik mit drei Phasen eingesetzt wird. Die symmetrische Sternschaltung wird entwickelt und die relevanten Leistungen werden berechnet.
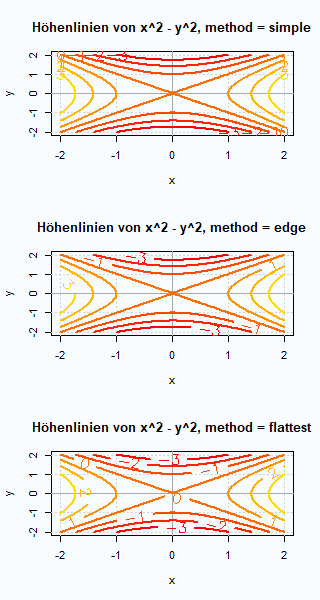
Die Funktion contour() ermöglicht es die Höhenlinien einer reellwertigen Funktion darzustellen, die auf einem zweidimensionalen Gebiet definiert ist. Die Höhenlinien geben manchmal den Graphen besser wieder als eine perspektivische dreidimensionale Darstellung wie sie etwa mit persp() erzeugt werden kann. An einfachen Beispielen werden die Eingabewerte von contour() erläutert.
Pünktlich zu Halloween, wenn Geistergeschichten und gruselige Legenden Hochkonjunktur haben, lohnt es sich, auch in der digitalen Welt nach verborgenen Geheimnissen zu suchen. Der Kauf einer Domain ist oft ein aufregender Schritt auf dem Weg zur eigenen Website, doch was, wenn diese Domain eine düstere Vergangenheit hat? Manche Domains tragen nämlich mehr als nur ihren Namen – sie bringen eine Geschichte voller Spam, Blacklistings oder sogar rechtlicher Probleme mit sich, die wie unsichtbare Geister die neue Website heimsuchen könnten.
Primitive Datentypen sind die Grundlage für Datenverarbeitung und -speicherung in Java, da sie einfache Werte effizient und ohne den Overhead von Objekten speichern. Dieser Artikel bietet eine Einführung in die grundlegenden Eigenschaften jedes primitiven Datentyps und erläutert Speicherbedarf sowie Wertebereiche.
Das Mono-Projekt hat überraschend die Verwaltung an WineHQ übergeben, was eine wichtige Phase im .NET-Ökosystem abschließt. Dieser Schritt hat Diskussionen über Monos Erbe und zukünftige Entwicklung angestoßen.
Bereit für das ultimative Textabenteuer? Mit Vim-Racer.com kannst du nicht nur deine Navigationskünste in Vim auf die Probe stellen, sondern dich auch in einem rasanten Wettkampf gegen andere Entwickler beweisen. Schalte den Turbo ein, fliege durch den Code und zeige, dass du der Schnellste auf der Tastatur bist – alles ganz ohne Fingerkrämpfe oder Emacs-Verirrungen!
In diesem Artikel werden wir vier verschiedene Methoden zur Listenfilterung in Python untersuchen: Iteration, die filter-Funktion, List Comprehension und die itertools-Bibliothek. Jede Methode hat ihre eigenen Stärken und Schwächen, wodurch sie für unterschiedliche Szenarien und Anwendungsfälle geeignet sind.
Convolutional Neural Networks (CNNs) sind eine der grundlegendsten und leistungsstärksten Methoden in der modernen Computer Vision. Sie ermöglichen es Computern, spezifische Objekte in zweidimensionalen Bildern zu erkennen und haben Anwendungen in Bereichen wie Bildklassifizierung, Objekterkennung und Gesichtserkennung revolutioniert. In diesem Artikel werden wir die grundlegenden Konzepte eines CNNs kennenlernen und anhand eines einfachen Beispiels demonstrieren, wie man ein eigenes CNN erstellen kann.
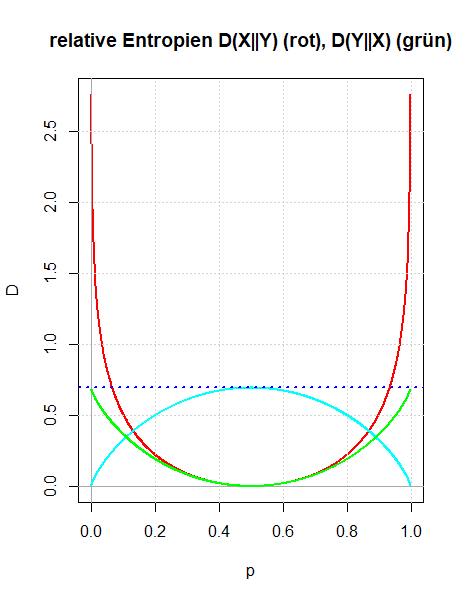
Es werden zwei Zugänge gezeigt, wie man die relative Entropie motivieren kann: Entweder als Verallgemeinerung der gegenseitigen Information oder indem man die Überlegungen Boltzmanns zur Definition der Entropie in dem Sinn verallgemeinert, dass man die Voraussetzung der Gleichwahrscheinlichkeit der Mikrozustände aufgibt. Die Bedeutung der relativen Entropie als einer Größe, die quantifiziert, wie unterschiedlich zwei Wahrscheinlichkeitsverteilungen sind, wird durch den zweiten Zugang besser verständlich.
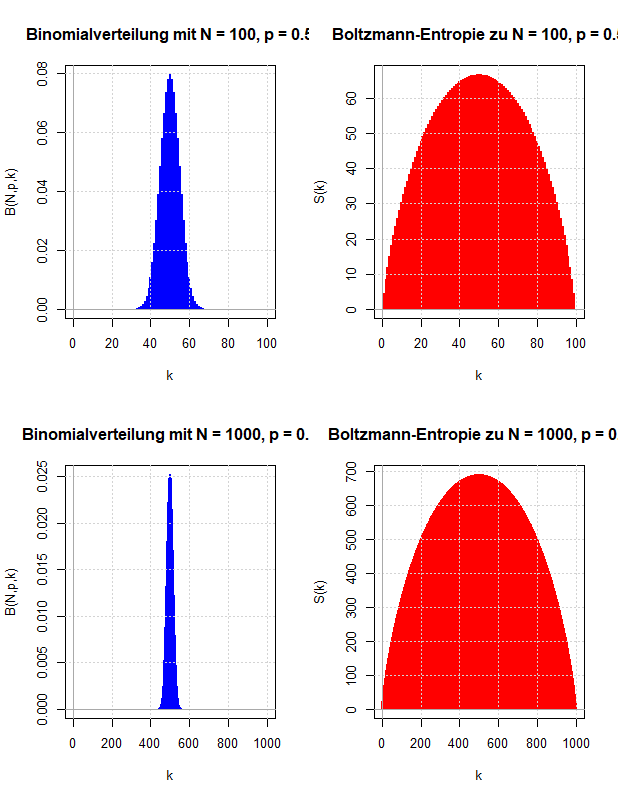
Ludwig Boltzmann gab eine mikroskopische Erklärung für die thermodynamische Entropie, die nach dem zweiten Hauptsatz der Thermodynamik niemals abnehmen kann. Diese Überlegungen werden verwendet, um zu motivieren, wie die Entropie der Wahrscheinlichkeitstheorie definiert wird, die die Ungewissheit über den Wert einer Zufallsvariable quantifizieren soll.
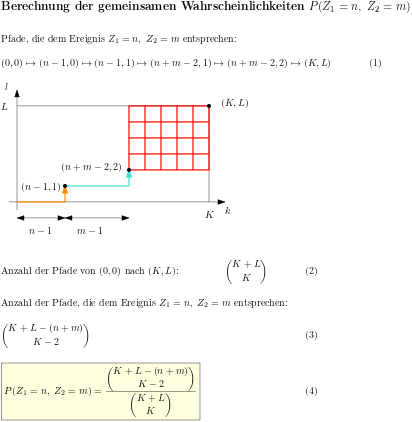
Die Entropie einer Zufallsvariable, die gemeinsame Entropie zweier Zufallsvariablen und die gegenseitige Information werden am Beispiel der Wartezeitprobleme beim Ziehen ohne Zurücklegen veranschaulicht. Dazu werden als Zufallsvariablen die Wartezeit bis zum ersten Treffer und die Wartezeit vom ersten bis zum zweiten Treffer verwendet.
YAML ("YAML Ain't Markup Language", mißverständlich auch "yet another markup language") ist eine Datenformatsprache, die in einer Vielzahl von Anwendungen eingesetzt wird, darunter die Konfiguration von Continuous Integration / Continuous Deployment (CI/CD) Pipelines, Docker- und Kubernetes-Konfigurationen sowie andere Softwareanwendungen. In diesem Artikel zeigen wir die Verwendung von SnakeYAML mit Java, einer leistungsstarken Bibliothek, die das Laden von YAML-Dateien als Map oder direkt in benutzerdefinierte Typen (POJOs) ermöglicht.