Schlagwort: Unabhängigkeit
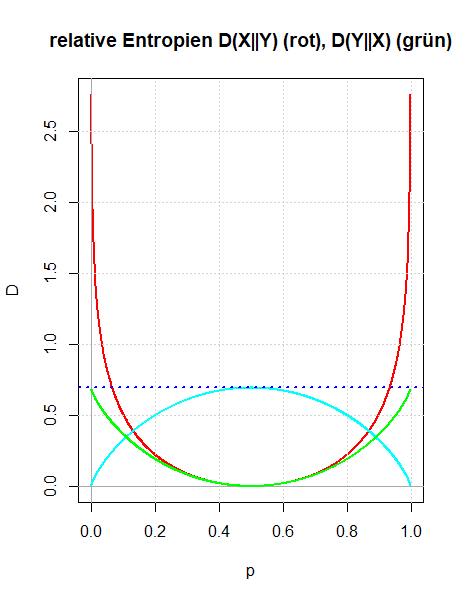
Es werden zwei Zugänge gezeigt, wie man die relative Entropie motivieren kann: Entweder als Verallgemeinerung der gegenseitigen Information oder indem man die Überlegungen Boltzmanns zur Definition der Entropie in dem Sinn verallgemeinert, dass man die Voraussetzung der Gleichwahrscheinlichkeit der Mikrozustände aufgibt. Die Bedeutung der relativen Entropie als einer Größe, die quantifiziert, wie unterschiedlich zwei Wahrscheinlichkeitsverteilungen sind, wird durch den zweiten Zugang besser verständlich.
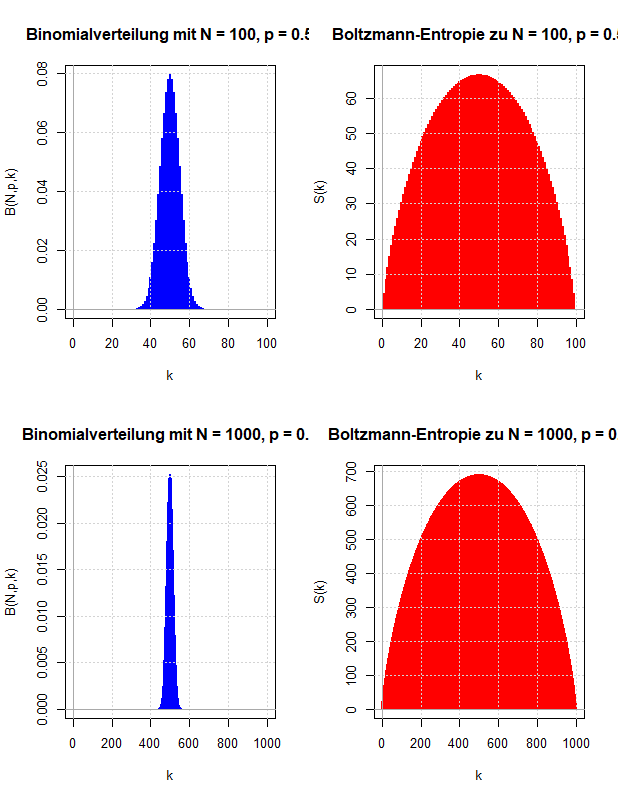
Ludwig Boltzmann gab eine mikroskopische Erklärung für die thermodynamische Entropie, die nach dem zweiten Hauptsatz der Thermodynamik niemals abnehmen kann. Diese Überlegungen werden verwendet, um zu motivieren, wie die Entropie der Wahrscheinlichkeitstheorie definiert wird, die die Ungewissheit über den Wert einer Zufallsvariable quantifizieren soll.
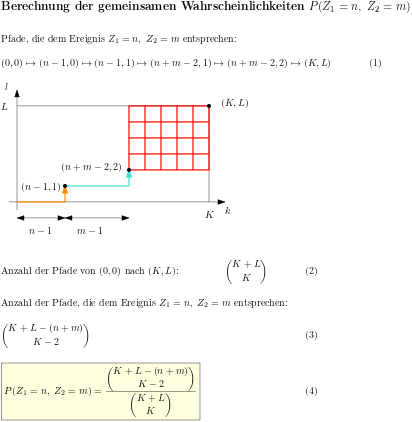
Die Entropie einer Zufallsvariable, die gemeinsame Entropie zweier Zufallsvariablen und die gegenseitige Information werden am Beispiel der Wartezeitprobleme beim Ziehen ohne Zurücklegen veranschaulicht. Dazu werden als Zufallsvariablen die Wartezeit bis zum ersten Treffer und die Wartezeit vom ersten bis zum zweiten Treffer verwendet.
Überträgt man den Begriff der Entropie einer Zufallsvariable auf die Wahrscheinlichkeitsverteilungen von zwei Zufallsvariablen, so ist es naheliegend die gemeinsame Entropie und die bedingte Entropie einzuführen, die über die Kettenregel miteinander verknüpft sind. Diese wiederum motiviert die Einführung einer neuen Größe, der gegenseitigen Information zweier Zufallsvariablen. Sie ist symmetrisch in den beiden Zufallsvariablen und beschreibt die Information, die in einer Zufallsvariable über die andere Zufallsvariable enthalten ist. An einfachen Beispielen wird die Definition der gegenseitigen Information motiviert und veranschaulicht.
Die Entropie wurde eingeführt als ein Maß für die Ungewissheit über den Ausgang eines Zufallsexperimentes. Entsprechend kann man eine bedingte Entropie definieren, wenn man die bedingten Wahrscheinlichkeiten verwendet, wobei man als Bedingung entweder ein Ereignis oder eine Zufallsvariable zulässt. Die Definition der bedingten Entropie und ihr Zusammenhang mit der gemeinsamen Entropie zweier Zufallsvariablen (Kettenregel) wird an einfachen Beispielen erläutert.
Akzeptiert man die Entropie als eine Kenngröße einer Wahrscheinlichkeitsverteilung, die die Ungewissheit über den Ausgang eines Zufallsexperimentes beschreibt, so wird man fordern, dass sich bei unabhängigen Zufallsexperimenten die Entropien addieren. Um diese Aussage schärfer formulieren zu können, wird die gemeinsame Entropie H(X, Y) von zwei Zufallsvariablen eingeführt. Es wird gezeigt, dass die übliche Definition der Entropie die Additivitätseigenschaft bei unabhängigen Zufallsvariablen X und Y besitzt.
Die geometrische Verteilung kann als Verteilung von Wartezeiten aufgefasst werden, wenn man einen Münzwurf solange wiederholt bis der erste Treffer eintritt: man berechnet die Wahrscheinlichkeiten der Anzahl der nötigen Würfe. Man kann dieses Wartezeitproblem verallgemeinern, indem man nicht bis zum ersten sondern bis zum r-ten Treffer wartet. Die Verteilung dieser Wartezeiten wird berechnet und die Eigenschaften der dabei entstehenden Verteilung wird untersucht.
Die Faltung von Wahrscheinlichkeitsmaßen ist eine der wichtigsten Begriffsbildungen, um Summen von unabhängigen Zufallsvariablen zu beschreiben, da sich mit ihr viele Eigenschaften von Zufallsvariablen und Wahrscheinlichkeitsverteilungen prägnant formulieren lassen und zahlreiche Bezüge zu anderen (scheinbar entfernten) Begriffen und Aussagen herstellen lassen. In diesem einführenden Kapitel wird auf exakte mathematische Definitionen und Beweise verzichtet, stattdessen soll der Begriff der Faltung an typischen Beispielen motiviert werden.
Beim mehrarmigen Banditen oder genauer k-armigen Banditen kann man ein Glücksspiel durch Betätigen eines Armes auslösen. Mathematisch modelliert werden sie durch Zufallsvariablen mit unterschiedlichen Erwartungswerten. Möchte man am k-armigen Banditen N Spiele durchführen und dabei einen möglichst hohen Gewinn erzielen, gerät man in ein Dilemma: Einerseits muss man alle Arme untersuchen, um ihre Kennzahlen zu schätzen (Exploration), andererseits möchte man möglichst oft den besten Arm betätigen (Exploitation). Im nächsten Kapitel werden dann Algorithmen entwickelt, die versuchen einen Kompromiss zwischen Exploration und Exploitation herzustellen.
