Die relative Entropie: Motivation, Definition und einfache Beispiele
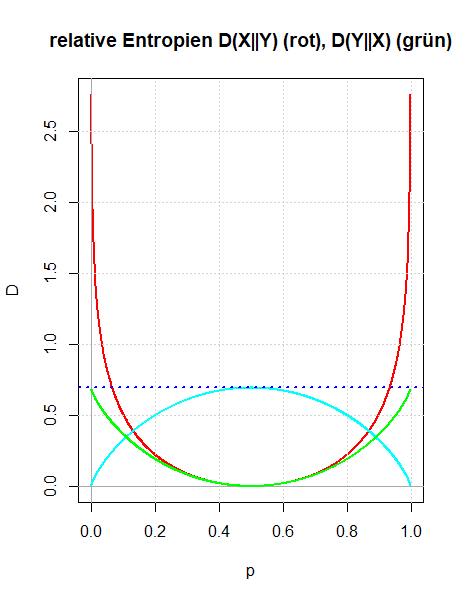
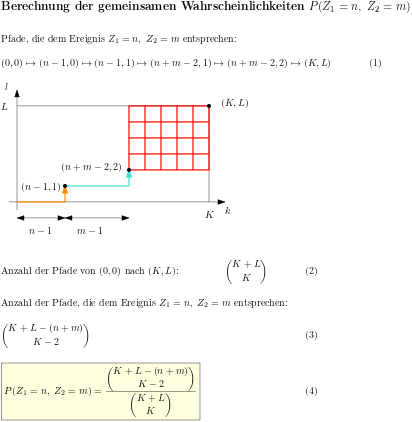
Es werden zwei Zugänge gezeigt, wie man die relative Entropie motivieren kann: Entweder als Verallgemeinerung der gegenseitigen Information oder indem man die Überlegungen Boltzmanns zur Definition der Entropie in dem Sinn verallgemeinert, dass man die Voraussetzung der Gleichwahrscheinlichkeit der Mikrozustände aufgibt. Die Bedeutung der relativen Entropie als einer Größe, die quantifiziert, wie unterschiedlich zwei Wahrscheinlichkeitsverteilungen sind, wird durch den zweiten Zugang besser verständlich.