Thermodynamik
Die Thermodynamik ist ein fundamentales Gebiet der Physik, das sich mit der Energieumwandlung und den Gesetzen der Wärme beschäftigt. Sie spielt eine wichtige Rolle in verschiedenen Bereichen der Naturwissenschaften und hat Anwendungen in der Chemie, Ingenieurwissenschaften und Biologie.
In der Thermodynamik werden die Eigenschaften von Systemen untersucht, die Energie mit ihrer Umgebung austauschen können. Ein grundlegendes Konzept ist der erste Hauptsatz der Thermodynamik, der besagt, dass die Energie in einem geschlossenen System erhalten bleibt und nur von einer Form in eine andere umgewandelt werden kann.
Ein weiteres wichtiges Gesetz ist der zweite Hauptsatz der Thermodynamik, der den Begriff der Entropie einführt. Entropie ist ein Maß für die Unordnung oder den Grad der Verteilung von Energie in einem System. Der zweite Hauptsatz besagt, dass die Entropie eines isolierten Systems im Laufe der Zeit zunimmt und ein Gleichgewichtszustand erreicht, in dem die Entropie maximal ist.
In unserem Artikel "Einführung einer Dynamik für das Modellsystem mit äquidistanten Energieniveaus und Simulationen zur statistischen Interpretation des zweiten Hauptsatzes der Thermodynamik" gehen wir genauer auf die statistische Interpretation des zweiten Hauptsatzes ein. Wir erklären, wie die Gleichwahrscheinlichkeit der Mikrozustände und die Definition der Boltzmann-Entropie zur statistischen Beschreibung von Systemen beitragen.
Des Weiteren behandeln wir in unseren Artikeln "Die innere Energie als thermodynamisches Potential" und "Die Berechnung der Entropie des idealen einatomigen Gases" weitere wichtige Konzepte der Thermodynamik. Wir zeigen, wie die innere Energie als thermodynamisches Potential genutzt wird und wie die Entropie für ein ideales einatomiges Gas berechnet werden kann.
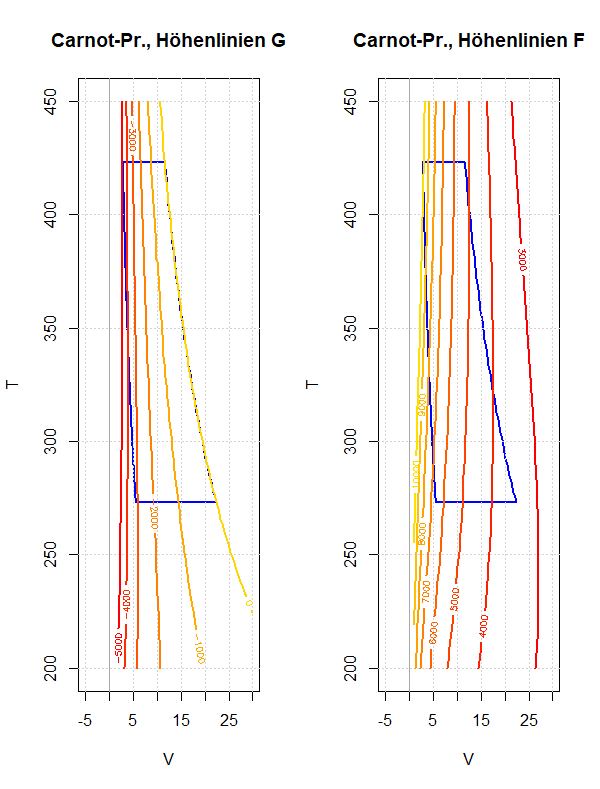
Am Beispiel des Carnot-Prozesses soll das Verhalten der freien und der gebundenen Energie während eines Umlaufs diskutiert werden. Dies soll die Bedeutung dieser thermodynamischen Potentiale besser verständlich machen; speziell ob und wie sie als Arbeitsfähigkeit beziehungsweise Wärmeinhalt eines Systems interpretiert werden können.
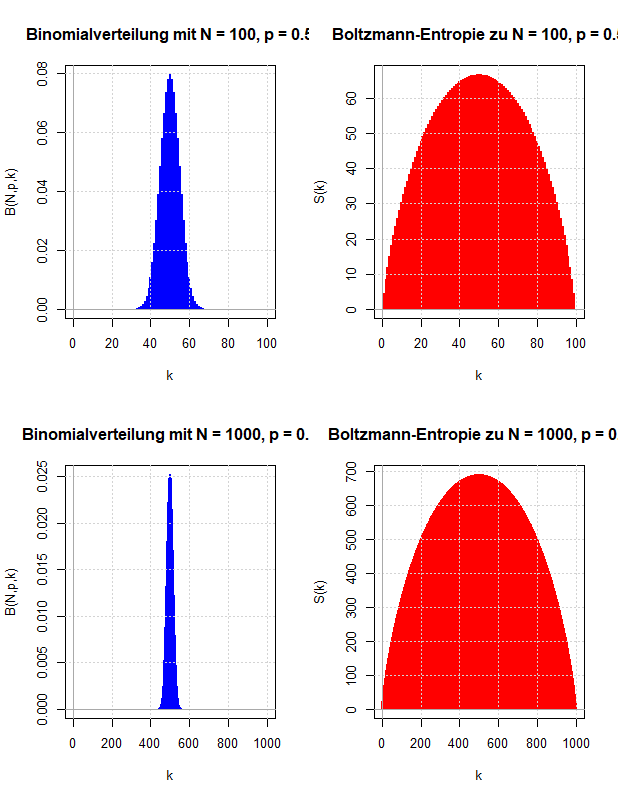
Ludwig Boltzmann gab eine mikroskopische Erklärung für die thermodynamische Entropie, die nach dem zweiten Hauptsatz der Thermodynamik niemals abnehmen kann. Diese Überlegungen werden verwendet, um zu motivieren, wie die Entropie der Wahrscheinlichkeitstheorie definiert wird, die die Ungewissheit über den Wert einer Zufallsvariable quantifizieren soll.
Am Beispiel der isochoren Erwärmung werden die Eigenschaften der freien Energie F = U - TS und der gebundenen Energie G = TS erläutert. Speziell wird gezeigt, wie man ihre Veränderung darstellen kann, wenn man vom US-Diagramm zum TS-Diagramm übergeht.
Die freie Energie F = U - TS ist die (negative) Legendre-Transformierte der inneren Energie U, wenn diese als Funktion der extensiven Variablen Entropie S und Volumen V dargestellt wird: U = U(S, V); die Legendre-Transformation wird dabei bezüglich der Variable S berechnet. Es ist dann leicht nachzuweisen, dass die freie Energie ein thermodynamisches Potential ist und dass die Änderung der freien Energie bei isothermen Zustandsänderungen mit der Zufuhr von mechanischer Arbeit übereinstimmt.
Mit Hilfe der freien Energie und der gebundenen Energie soll die innere Energie in zwei Anteile zerlegt werden: Die freie Energie soll allein durch die Zufuhr von mechanischer Arbeit und die gebundene Energie allein durch die Zufuhr von Wärme verändert werden. Diese Zerlegung lässt sich allerdings nur für isotherme Prozesse durchführen. Die Eigenschaften der freien und gebundenen Energie werden für die isotherme Zustandsänderung und andere einfache Prozesse diskutiert.
Mit dem Druckausgleich (also zwei Kammern mit einer beweglichen Trennwand, in der sich anfangs Gase mit unterschiedlichem Druck befinden) lassen sich zahlreiche Aspekte der Entropie und allgemeiner der Thermodynamik demonstrieren (reversible und irreversible Prozessführung, Eindeutigkeit des Endzustandes, Maximum der Entropie, Temperatur- und Volumenabhängigkeit der Entropie).
Wird die innere Energie als Funktion der extensiven Variablen dargestellt, enthält sie sämtliche Eigenschaften des entsprechenden thermodynamischen Systems; dies rechtfertigt die innere Energie als thermodynamisches Potential zu bezeichnen. Untersucht man speziell die innere Energie bei adiabatischen Zustandsänderungen, so kann man leicht motivieren, weshalb andere thermodynamische Potentiale (wie freie Energie oder Enthalpie) eingeführt werden. Am idealen einatomigen Gas werden diese Eigenschaften der inneren Energie demonstriert.
Der Carnot-Prozess ist sowohl inhaltlich als auch methodisch wichtig für die Thermodynamik: Seine Analyse liefert zahlreiche Einsichten in ihre Konzepte, Argumentationsweisen und technische Anwendungen.
Für das ideale einatomige Gas werden die Zusammenhänge zwischen den Hauptsätzen der Thermodynamik und den Zustandsgleichungen (thermische und kalorische Zustandsgleichung) diskutiert und angewendet, um die Entropie in verschiedenen Darstellungen zu berechnen. Illustriert werden die Herleitungen an speziellen Zustandsänderungen (isotherm, isochor, adiabatisch, freie Expansion).
Es werden Simulationen zum Temperaturausgleich durchgeführt: Das Modellsystem mit äquidistanten Energieniveaus wird in zwei Teilsysteme zerlegt, die anfangs unterschiedliche Energie haben. Es entwickelt sich unter einer einfachen Dynamik, bei der zufällig zwei Moleküle ausgewählt werden, die ein Energiequant austauschen.
Die Ergebnisse der Simulationen sollen die Konzepte illustrieren, mit denen die statistische Mechanik einen irreversiblen Vorgang beschreibt, der in der phänomenologischen Thermodynamik als Paradebeispiel für den zweiten Hauptsatz dient.
Das Modellsystem mit äquidistanten Energieniveaus wird mit einer einfachen Dynamik ausgestattet, die es erlaubt Energie zwischen zwei Molekülen auszutauschen. Damit lässt sich beobachten, welche Folge von Zuständen das System einnimmt, wenn man es in einem unwahrscheinlichen Mikrozustand startet. Die vorgestellten Simulationen und ihre Auswertung liefern weitere Illustrationen der Konzepte der statistischen Mechanik: Mikro- und Makrozustände, statistische Interpretation des zweiten Hauptsatzes der Thermodynamik.
Die Konzepte Mikrozustand, Makrozustand, Gleichverteilungs-Postulat und Boltzmann-Entropie der statistischen Mechanik werden mit Hilfe einfacher Simulationen erläutert.
Für das Modellsystem mit unabhängigen Teilchen, die äquidistante Energieniveaus besitzen, werden die wichtigsten statistischen und thermodynamischen Größen berechnet.
In den vorausgegangenen Kapiteln wurden die Abzählprobleme behandelt, die sich ergeben, wenn ein thermodynamisches System entweder auf der Ebene der Mikrozustände oder der Makrozustände beschrieben wird. Vergleicht man diese Ergebnisse mit den Gleichungen der phänomenologischen Thermodynamik, kann man eine statistische Definition der Entropie ableiten und damit eine (statistische) Erklärung des zweiten Hauptsatzes der Thermodynamik liefern. Die Boltzmann-Entropie wird mit Hilfe der Anzahl der Mikrozustände pro Makrozustand definiert und besitzt die Eigenschaften, die man innerhalb der Thermodynamik an die Entropie stellt.
Es werden zwei Anwendungen des Entropiesatzes besprochen. Zum Einen warum Wärme immer vom wärmeren zum kälteren Körper strömt und niemals umgekehrt. Zum Anderen die Entropieproduktion bei einem Mischvorgang. Dabei wird geklärt, für welchen Rechenschritt welcher Hauptsatz der Thermodynamik verwendet wird.
Für ein einfaches Modellsystem wird untersucht, welcher Makrozustand durch die meisten Mikrozustände realisiert wird und wie sich dieser Makrozustand charakterisieren lässt. Dabei werden die zugehörigen Abzählprobleme näherungsweise gelöst, da ihre exakte Lösung nur für sehr kleine Teilchenzahlen möglich ist. Die Methoden für diese Näherungen werden ausführlich besprochen: Stirling-Formel und Suche nach dem Maximum eines Multinomialkoeffizienten unter Nebenbedingung (mit Lagrange-Multiplikatoren).
Die statistische Mechanik versucht das makroskopische Verhalten von Materie zu erklären, indem anstelle einer detaillierten mikroskopischen Beschreibung Vergröberungen vorgenommen und statistische Methoden angewendet werden. Ein zentrales Konzept ist dabei die Definition von Makrozuständen, die Äquivalenzklassen auf der Menge der Mikrozustände erzeugen. Dieses Konzept und welche Abzählprobleme dabei entstehen, wird an einem einfachen Modellsystem erklärt.