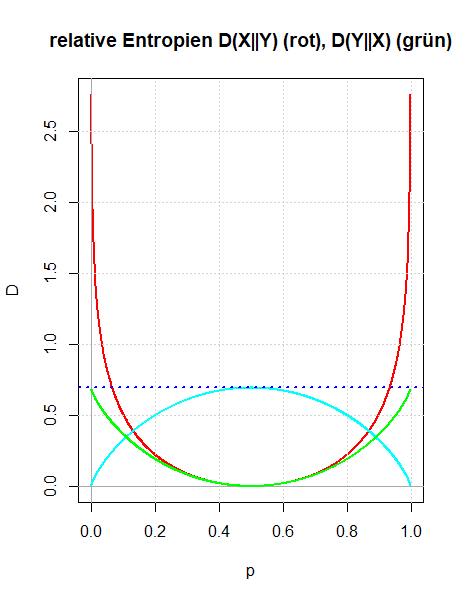
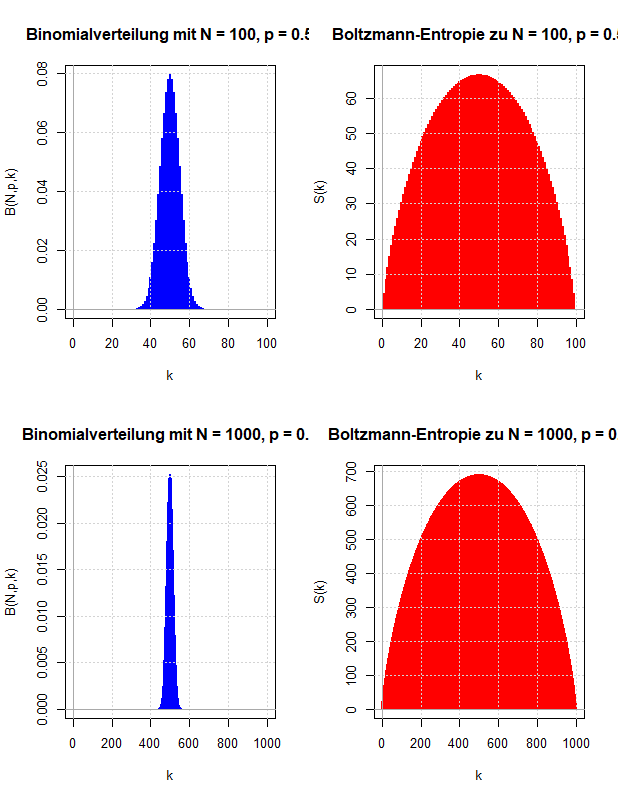
Es werden zwei Zugänge gezeigt, wie man die relative Entropie motivieren kann: Entweder als Verallgemeinerung der gegenseitigen Information oder indem man die Überlegungen Boltzmanns zur Definition der Entropie in dem Sinn verallgemeinert, dass man die Voraussetzung der Gleichwahrscheinlichkeit der Mikrozustände aufgibt. Die Bedeutung der relativen Entropie als einer Größe, die quantifiziert, wie unterschiedlich zwei Wahrscheinlichkeitsverteilungen sind, wird durch den zweiten Zugang besser verständlich.
Ludwig Boltzmann gab eine mikroskopische Erklärung für die thermodynamische Entropie, die nach dem zweiten Hauptsatz der Thermodynamik niemals abnehmen kann. Diese Überlegungen werden verwendet, um zu motivieren, wie die Entropie der Wahrscheinlichkeitstheorie definiert wird, die die Ungewissheit über den Wert einer Zufallsvariable quantifizieren soll.
Die Zufallsexperimente Ziehen mit Zurücklegen beziehungsweise Ziehen ohne Zurücklegen werden umformuliert in eine Zufallsbewegung auf einem Gitter. Dadurch lassen sich viele Herleitungen besser veranschaulichen. Gezeigt wird dies hier für die Verteilungen der Zufallsvariablen, die die Anzahl der Treffer oder die Wartezeit bis zu einem bestimmten Treffer beschreiben.
Es werden die Wartezeitprobleme bei den beiden Zufallsexperimenten Ziehen mit Zurücklegen beziehungsweise Ziehen ohne Zurücklegen untersucht.
Bei diesen Zufallsexperimenten befinden sich in einer Urne Treffer und Nieten. Mit Wartezeitproblem ist gemeint, dass man eine Zufallsvariable definiert, die angibt nach wie vielen Zügen der r-te Treffer aus der Urne entnommen wird. Zur Vorbereitung werden die Zusammenhänge zwischen Binomialverteilung, geometrischer Verteilung und hyper-geometrischer Verteilung gezeigt.
Die geometrische Verteilung kann als Verteilung von Wartezeiten aufgefasst werden, wenn man einen Münzwurf solange wiederholt bis der erste Treffer eintritt: man berechnet die Wahrscheinlichkeiten der Anzahl der nötigen Würfe. Man kann dieses Wartezeitproblem verallgemeinern, indem man nicht bis zum ersten sondern bis zum r-ten Treffer wartet. Die Verteilung dieser Wartezeiten wird berechnet und die Eigenschaften der dabei entstehenden Verteilung wird untersucht.
Das Abzählproblem "Ziehen ohne Zurücklegen" wird unter der Annahme betrachtet, dass sich in der Urne zwei Arten von Objekten befinden (etwa K Nieten und L Treffer). Berechnet wird die Anzahl der möglichen Ergebnisse, wenn N-mal ein Los aus der Urne gezogen wird und dabei die Reihenfolge der Ergebnisse beachtet wird.
Ebenso wird gezeigt, wie man die möglichen Ergebnisse mit Hilfe des Hamming-Abstandes charakterisieren und mit Hilfe des N-dimensionalen Hyperwürfels und im Pascalschen Dreieck veranschaulichen kann. In den R-Skripten werden Algorithmen für das Abzählproblem und die Berechnung der möglichen Ergebnisse vorgestellt und diskutiert.
Binomialkoeffizienten und einige einfache Anwendungen in Abzählproblemen (wie die Anzahl der möglichen Ergebnisse beim Zahlenlotto) wurden bereits in den Begriffsbildungen der Kombinatorik vorgestellt. Hier werden die grundlegenden Eigenschaften der Binomialkoeffizienten diskutiert: die Pascalsche Rekursionsformel, der Aufbau des Pascalschen Dreiecks, der binomische Satz. Binomialkoeffizienten treten in unüberschaubar vielen Bereichen der Mathematik auf und ihr Auftreten sollte immer als Hinweis auf - mehr oder weniger offensichtliche - Querverbindungen verstanden werden. Als Beispiel einer dieser Querverbindungen wird der Zusammenhang der Binomialkoeffizienten mit dem n-dimensionalen Hyperwürfel diskutiert.
Kombinationen mit Wiederholungen treten in mehreren Abzählproblemen auf, die zunächst sehr unterschiedlich wirken. Es wird ihre Äquivalenz gezeigt und die Formel hergeleitet, wie man die Anzahl aller Kombinationen mit Wiederholungen berechnet. Dazu verwendet man die Methode Stars and Bars. In den R-Skripten wird ein einfacher Algorithmus gezeigt, wie man die Menge alle Kombinationen mit Wiederholungen rekursiv berechnet.
Nachdem im letzten Kapitel Beispiele für einfache Abzählprobleme vorgestellt wurden, werden jetzt die Grundbegriffe der Kombinatorik, nämlich Variation, Permutation und Kombination eingeführt, systematisch untersucht und an weiteren einfachen Beispielen erläutert.
An einfachen Abzählproblemen beim Würfeln wird gezeigt, wie man in der Kombinatorik systematisch vorgeht, um Abzählprobleme zu klassifizieren und allgemeine Formeln zur Berechnung der Anzahl der Realisierungen gewisser Ereignisse herzuleiten. In den R-Skripten werden Beispiele gezeigt, wie man solche Probleme auch ohne Kenntnisse aus der Kombinatorik mit roher Gewalt (brute force-Algorithmen) lösen kann.