In einem Artikel zur Einführung einer Dynamik für ein Modellsystem mit äquidistanten Energieniveaus und Simulationen zur statistischen Interpretation des zweiten Hauptsatzes der Thermodynamik wird die Bedeutung der Entropie für die Beschreibung von thermodynamischen Prozessen verdeutlicht. Dabei wird insbesondere auf die Boltzmann-Entropie eingegangen, die auf der Gleichwahrscheinlichkeit der Mikrozustände eines Systems beruht.
Ein weiterer Artikel beschäftigt sich mit der Berechnung der Entropie des idealen einatomigen Gases und gibt Einblicke in die statistische Interpretation des zweiten Hauptsatzes der Thermodynamik. Hier werden auch einfache Simulationen zur Boltzmann-Entropie vorgestellt.
Die Entropie spielt auch eine Rolle bei der Berechnung der thermodynamischen und statistischen Größen für das Modellsystem mit äquidistanten Energieniveaus.
Hier werden die Eigenschaften der thermodynamischen Potentiale, insbesondere der freien Energie, erläutert.
In der Mathematik wird die Entropie zu einer Größe abstrahiert, welche die Unsicherheit über den Ausgang eines Zufallsexperimentes beschreibt. Sie wird in einem Artikel zur Berechnung der Entropie einer diskreten Wahrscheinlichkeitsverteilung eingeführt und es werden einfache Beispiele zur Veranschaulichung gezeigt.
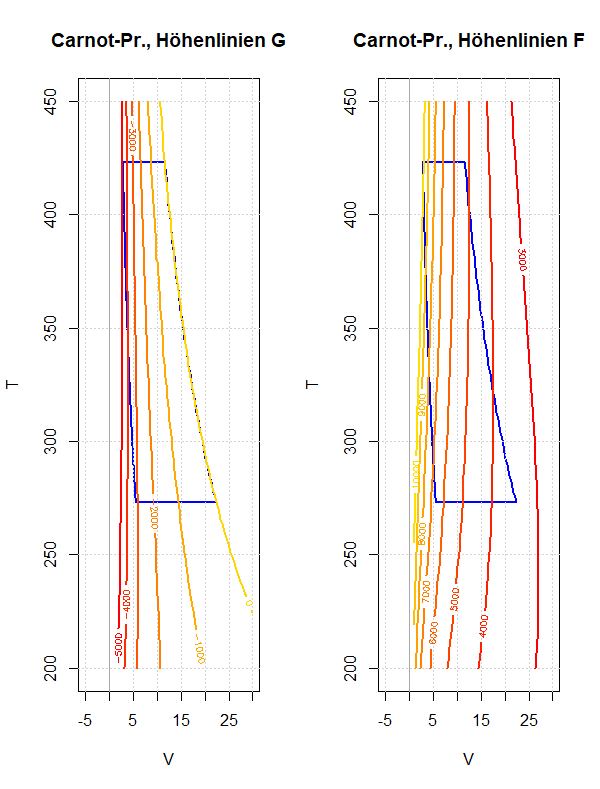
Am Beispiel des Carnot-Prozesses soll das Verhalten der freien und der gebundenen Energie während eines Umlaufs diskutiert werden. Dies soll die Bedeutung dieser thermodynamischen Potentiale besser verständlich machen; speziell ob und wie sie als Arbeitsfähigkeit beziehungsweise Wärmeinhalt eines Systems interpretiert werden können.
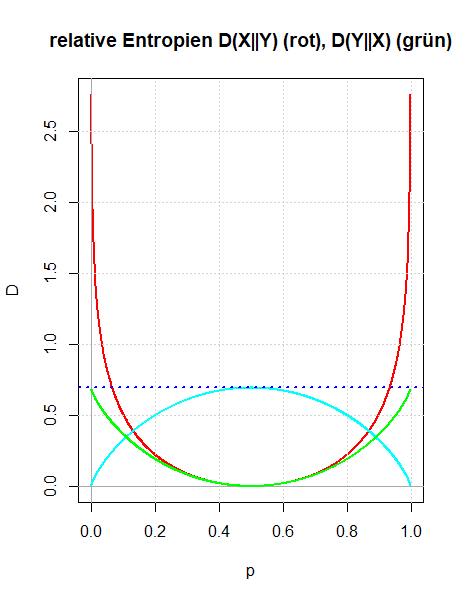
Es werden zwei Zugänge gezeigt, wie man die relative Entropie motivieren kann: Entweder als Verallgemeinerung der gegenseitigen Information oder indem man die Überlegungen Boltzmanns zur Definition der Entropie in dem Sinn verallgemeinert, dass man die Voraussetzung der Gleichwahrscheinlichkeit der Mikrozustände aufgibt. Die Bedeutung der relativen Entropie als einer Größe, die quantifiziert, wie unterschiedlich zwei Wahrscheinlichkeitsverteilungen sind, wird durch den zweiten Zugang besser verständlich.
Ludwig Boltzmann gab eine mikroskopische Erklärung für die thermodynamische Entropie, die nach dem zweiten Hauptsatz der Thermodynamik niemals abnehmen kann. Diese Überlegungen werden verwendet, um zu motivieren, wie die Entropie der Wahrscheinlichkeitstheorie definiert wird, die die Ungewissheit über den Wert einer Zufallsvariable quantifizieren soll.
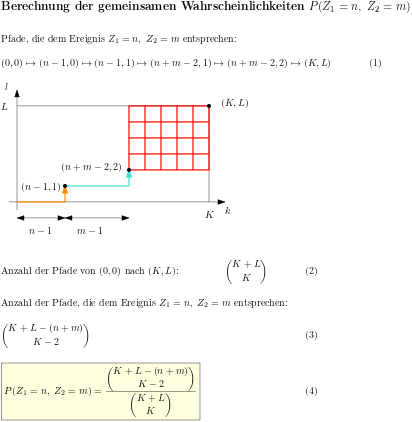
Die Entropie einer Zufallsvariable, die gemeinsame Entropie zweier Zufallsvariablen und die gegenseitige Information werden am Beispiel der Wartezeitprobleme beim Ziehen ohne Zurücklegen veranschaulicht. Dazu werden als Zufallsvariablen die Wartezeit bis zum ersten Treffer und die Wartezeit vom ersten bis zum zweiten Treffer verwendet.
Überträgt man den Begriff der Entropie einer Zufallsvariable auf die Wahrscheinlichkeitsverteilungen von zwei Zufallsvariablen, so ist es naheliegend die gemeinsame Entropie und die bedingte Entropie einzuführen, die über die Kettenregel miteinander verknüpft sind. Diese wiederum motiviert die Einführung einer neuen Größe, der gegenseitigen Information zweier Zufallsvariablen. Sie ist symmetrisch in den beiden Zufallsvariablen und beschreibt die Information, die in einer Zufallsvariable über die andere Zufallsvariable enthalten ist. An einfachen Beispielen wird die Definition der gegenseitigen Information motiviert und veranschaulicht.
Die Entropie wurde eingeführt als ein Maß für die Ungewissheit über den Ausgang eines Zufallsexperimentes. Entsprechend kann man eine bedingte Entropie definieren, wenn man die bedingten Wahrscheinlichkeiten verwendet, wobei man als Bedingung entweder ein Ereignis oder eine Zufallsvariable zulässt. Die Definition der bedingten Entropie und ihr Zusammenhang mit der gemeinsamen Entropie zweier Zufallsvariablen (Kettenregel) wird an einfachen Beispielen erläutert.
Akzeptiert man die Entropie als eine Kenngröße einer Wahrscheinlichkeitsverteilung, die die Ungewissheit über den Ausgang eines Zufallsexperimentes beschreibt, so wird man fordern, dass sich bei unabhängigen Zufallsexperimenten die Entropien addieren.
Um diese Aussage schärfer formulieren zu können, wird die gemeinsame Entropie H(X, Y) von zwei Zufallsvariablen eingeführt.
Es wird gezeigt, dass die übliche Definition der Entropie die Additivitätseigenschaft bei unabhängigen Zufallsvariablen X und Y besitzt.
Am Beispiel der isochoren Erwärmung werden die Eigenschaften der freien Energie F = U - TS und der gebundenen Energie G = TS erläutert. Speziell wird gezeigt, wie man ihre Veränderung darstellen kann, wenn man vom US-Diagramm zum TS-Diagramm übergeht.
Die freie Energie F = U - TS ist die (negative) Legendre-Transformierte der inneren Energie U, wenn diese als Funktion der extensiven Variablen Entropie S und Volumen V dargestellt wird: U = U(S, V); die Legendre-Transformation wird dabei bezüglich der Variable S berechnet. Es ist dann leicht nachzuweisen, dass die freie Energie ein thermodynamisches Potential ist und dass die Änderung der freien Energie bei isothermen Zustandsänderungen mit der Zufuhr von mechanischer Arbeit übereinstimmt.
Mit Hilfe der freien Energie und der gebundenen Energie soll die innere Energie in zwei Anteile zerlegt werden: Die freie Energie soll allein durch die Zufuhr von mechanischer Arbeit und die gebundene Energie allein durch die Zufuhr von Wärme verändert werden. Diese Zerlegung lässt sich allerdings nur für isotherme Prozesse durchführen. Die Eigenschaften der freien und gebundenen Energie werden für die isotherme Zustandsänderung und andere einfache Prozesse diskutiert.
Mit dem Druckausgleich (also zwei Kammern mit einer beweglichen Trennwand, in der sich anfangs Gase mit unterschiedlichem Druck befinden) lassen sich zahlreiche Aspekte der Entropie und allgemeiner der Thermodynamik demonstrieren (reversible und irreversible Prozessführung, Eindeutigkeit des Endzustandes, Maximum der Entropie, Temperatur- und Volumenabhängigkeit der Entropie).
Wird die innere Energie als Funktion der extensiven Variablen dargestellt, enthält sie sämtliche Eigenschaften des entsprechenden thermodynamischen Systems; dies rechtfertigt die innere Energie als thermodynamisches Potential zu bezeichnen. Untersucht man speziell die innere Energie bei adiabatischen Zustandsänderungen, so kann man leicht motivieren, weshalb andere thermodynamische Potentiale (wie freie Energie oder Enthalpie) eingeführt werden. Am idealen einatomigen Gas werden diese Eigenschaften der inneren Energie demonstriert.
Der Carnot-Prozess ist sowohl inhaltlich als auch methodisch wichtig für die Thermodynamik: Seine Analyse liefert zahlreiche Einsichten in ihre Konzepte, Argumentationsweisen und technische Anwendungen.
Für das ideale einatomige Gas werden die Zusammenhänge zwischen den Hauptsätzen der Thermodynamik und den Zustandsgleichungen (thermische und kalorische Zustandsgleichung) diskutiert und angewendet, um die Entropie in verschiedenen Darstellungen zu berechnen. Illustriert werden die Herleitungen an speziellen Zustandsänderungen (isotherm, isochor, adiabatisch, freie Expansion).
Die Definition der Entropie eines Wahrscheinlichkeitsmaßes oder einer Zufallsvariable wird an einfachen Beispielen erläutert. Es wird diskutiert, dass die Entropie kein Streuungsmaß ist (wie die Standardabweichung), sondern die Ungewissheit (oder Unbestimmtheit) des Ausgangs eines Zufallsexperimentes beschreibt.
Es werden Simulationen zum Temperaturausgleich durchgeführt: Das Modellsystem mit äquidistanten Energieniveaus wird in zwei Teilsysteme zerlegt, die anfangs unterschiedliche Energie haben. Es entwickelt sich unter einer einfachen Dynamik, bei der zufällig zwei Moleküle ausgewählt werden, die ein Energiequant austauschen.
Die Ergebnisse der Simulationen sollen die Konzepte illustrieren, mit denen die statistische Mechanik einen irreversiblen Vorgang beschreibt, der in der phänomenologischen Thermodynamik als Paradebeispiel für den zweiten Hauptsatz dient.
Das Modellsystem mit äquidistanten Energieniveaus wird mit einer einfachen Dynamik ausgestattet, die es erlaubt Energie zwischen zwei Molekülen auszutauschen. Damit lässt sich beobachten, welche Folge von Zuständen das System einnimmt, wenn man es in einem unwahrscheinlichen Mikrozustand startet. Die vorgestellten Simulationen und ihre Auswertung liefern weitere Illustrationen der Konzepte der statistischen Mechanik: Mikro- und Makrozustände, statistische Interpretation des zweiten Hauptsatzes der Thermodynamik.
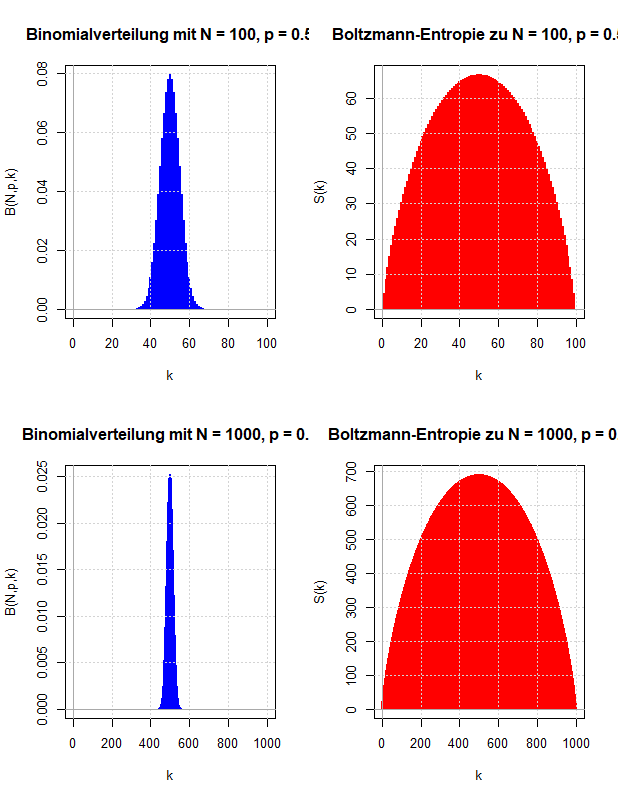
Die Konzepte Mikrozustand, Makrozustand, Gleichverteilungs-Postulat und Boltzmann-Entropie der statistischen Mechanik werden mit Hilfe einfacher Simulationen erläutert.
Für das Modellsystem mit unabhängigen Teilchen, die äquidistante Energieniveaus besitzen, werden die wichtigsten statistischen und thermodynamischen Größen berechnet.
In den vorausgegangenen Kapiteln wurden die Abzählprobleme behandelt, die sich ergeben, wenn ein thermodynamisches System entweder auf der Ebene der Mikrozustände oder der Makrozustände beschrieben wird. Vergleicht man diese Ergebnisse mit den Gleichungen der phänomenologischen Thermodynamik, kann man eine statistische Definition der Entropie ableiten und damit eine (statistische) Erklärung des zweiten Hauptsatzes der Thermodynamik liefern. Die Boltzmann-Entropie wird mit Hilfe der Anzahl der Mikrozustände pro Makrozustand definiert und besitzt die Eigenschaften, die man innerhalb der Thermodynamik an die Entropie stellt.
Es werden zwei Anwendungen des Entropiesatzes besprochen. Zum Einen warum Wärme immer vom wärmeren zum kälteren Körper strömt und niemals umgekehrt. Zum Anderen die Entropieproduktion bei einem Mischvorgang. Dabei wird geklärt, für welchen Rechenschritt welcher Hauptsatz der Thermodynamik verwendet wird.