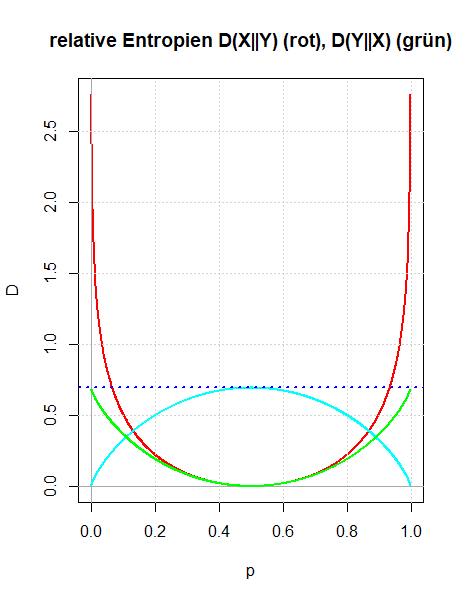
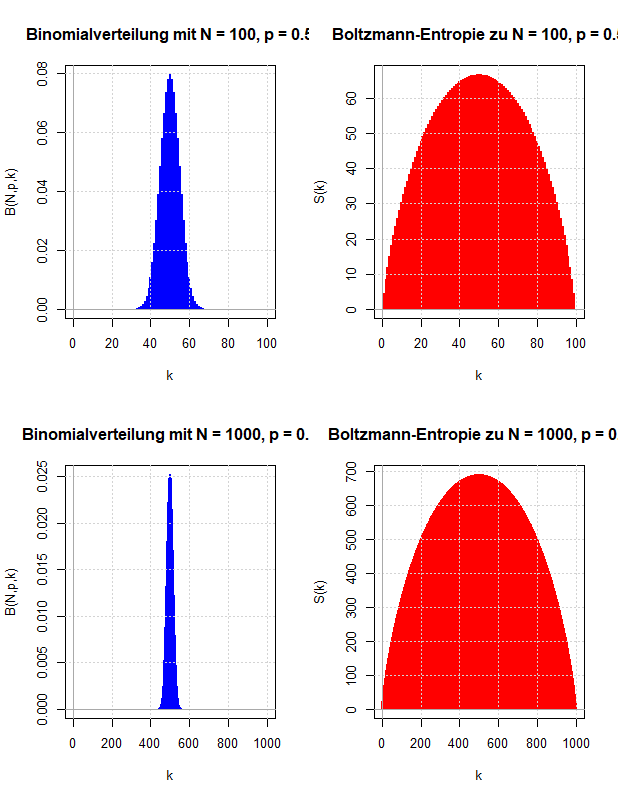
Es werden zwei Zugänge gezeigt, wie man die relative Entropie motivieren kann: Entweder als Verallgemeinerung der gegenseitigen Information oder indem man die Überlegungen Boltzmanns zur Definition der Entropie in dem Sinn verallgemeinert, dass man die Voraussetzung der Gleichwahrscheinlichkeit der Mikrozustände aufgibt. Die Bedeutung der relativen Entropie als einer Größe, die quantifiziert, wie unterschiedlich zwei Wahrscheinlichkeitsverteilungen sind, wird durch den zweiten Zugang besser verständlich.
Ludwig Boltzmann gab eine mikroskopische Erklärung für die thermodynamische Entropie, die nach dem zweiten Hauptsatz der Thermodynamik niemals abnehmen kann. Diese Überlegungen werden verwendet, um zu motivieren, wie die Entropie der Wahrscheinlichkeitstheorie definiert wird, die die Ungewissheit über den Wert einer Zufallsvariable quantifizieren soll.
Es werden Simulationen zum Temperaturausgleich durchgeführt: Das Modellsystem mit äquidistanten Energieniveaus wird in zwei Teilsysteme zerlegt, die anfangs unterschiedliche Energie haben. Es entwickelt sich unter einer einfachen Dynamik, bei der zufällig zwei Moleküle ausgewählt werden, die ein Energiequant austauschen.
Die Ergebnisse der Simulationen sollen die Konzepte illustrieren, mit denen die statistische Mechanik einen irreversiblen Vorgang beschreibt, der in der phänomenologischen Thermodynamik als Paradebeispiel für den zweiten Hauptsatz dient.
Das Modellsystem mit äquidistanten Energieniveaus wird mit einer einfachen Dynamik ausgestattet, die es erlaubt Energie zwischen zwei Molekülen auszutauschen. Damit lässt sich beobachten, welche Folge von Zuständen das System einnimmt, wenn man es in einem unwahrscheinlichen Mikrozustand startet. Die vorgestellten Simulationen und ihre Auswertung liefern weitere Illustrationen der Konzepte der statistischen Mechanik: Mikro- und Makrozustände, statistische Interpretation des zweiten Hauptsatzes der Thermodynamik.
Die Konzepte Mikrozustand, Makrozustand, Gleichverteilungs-Postulat und Boltzmann-Entropie der statistischen Mechanik werden mit Hilfe einfacher Simulationen erläutert.
Für das Modellsystem mit unabhängigen Teilchen, die äquidistante Energieniveaus besitzen, werden die wichtigsten statistischen und thermodynamischen Größen berechnet.
Nach dem Postulat der statistischen Mechanik besitzen alle Mikrozustände, die ein System annehmen kann, die gleiche Wahrscheinlichkeit. Für zahlreiche Simulationen benötigt man einen Zufallsgenerator, der diese gleichverteilten Mikrozustände erzeugt. Dieser Zufallsgenerator wird in der Programmiersprache R entwickelt, die Erklärungen sind aber so allgemein gehalten, dass man sie leicht in eine andere Programmiersprache übersetzen kann.
In den vorausgegangenen Kapiteln wurden die Abzählprobleme behandelt, die sich ergeben, wenn ein thermodynamisches System entweder auf der Ebene der Mikrozustände oder der Makrozustände beschrieben wird. Vergleicht man diese Ergebnisse mit den Gleichungen der phänomenologischen Thermodynamik, kann man eine statistische Definition der Entropie ableiten und damit eine (statistische) Erklärung des zweiten Hauptsatzes der Thermodynamik liefern. Die Boltzmann-Entropie wird mit Hilfe der Anzahl der Mikrozustände pro Makrozustand definiert und besitzt die Eigenschaften, die man innerhalb der Thermodynamik an die Entropie stellt.
Für ein einfaches Modellsystem wird untersucht, welcher Makrozustand durch die meisten Mikrozustände realisiert wird und wie sich dieser Makrozustand charakterisieren lässt. Dabei werden die zugehörigen Abzählprobleme näherungsweise gelöst, da ihre exakte Lösung nur für sehr kleine Teilchenzahlen möglich ist. Die Methoden für diese Näherungen werden ausführlich besprochen: Stirling-Formel und Suche nach dem Maximum eines Multinomialkoeffizienten unter Nebenbedingung (mit Lagrange-Multiplikatoren).
Die statistische Mechanik versucht das makroskopische Verhalten von Materie zu erklären, indem anstelle einer detaillierten mikroskopischen Beschreibung Vergröberungen vorgenommen und statistische Methoden angewendet werden. Ein zentrales Konzept ist dabei die Definition von Makrozuständen, die Äquivalenzklassen auf der Menge der Mikrozustände erzeugen. Dieses Konzept und welche Abzählprobleme dabei entstehen, wird an einem einfachen Modellsystem erklärt.