Artikel aus dem Jahr 2025
Insgesamt 15, zur Liste aller Artikel aus diesem Jahr.
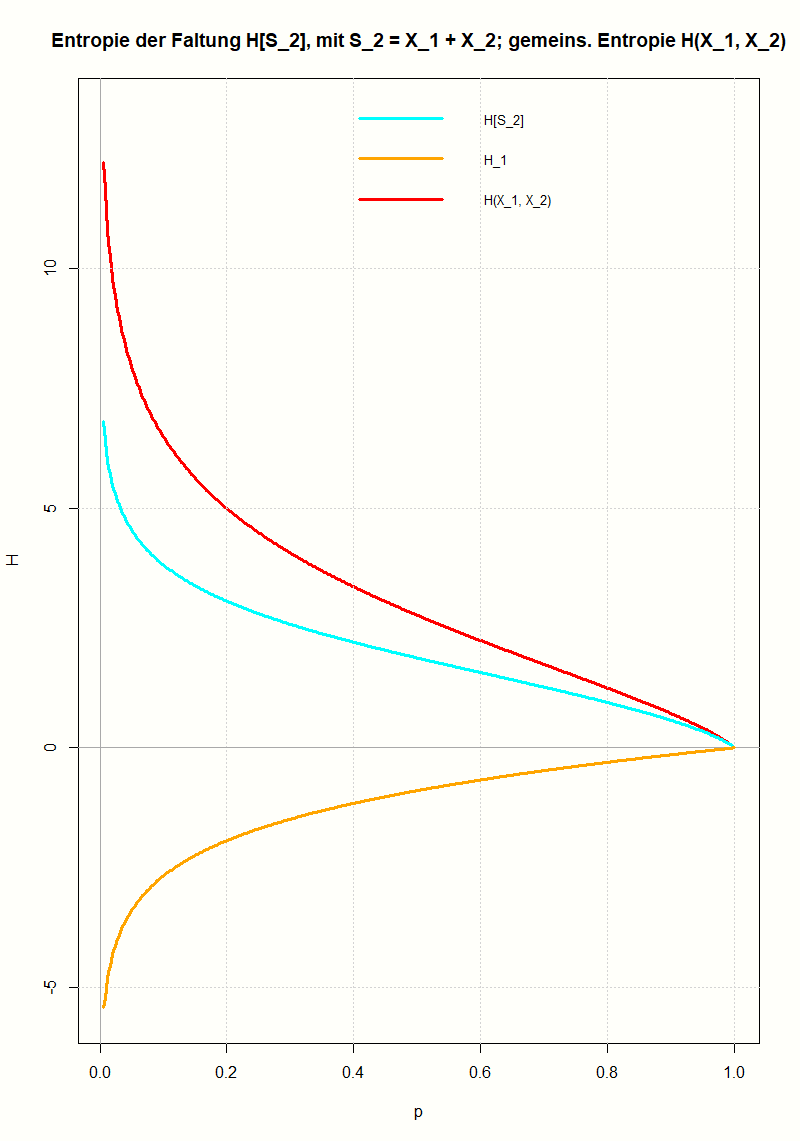
Am Beispiel der geometrischen Verteilung wird gezeigt, wie man die Entropie einer Faltung berechnet und wie sie mit den Entropien der Ausgangsverteilungen zusammenhängt. Mit Hilfe der Log-Summen-Ungleichung (einer Folgerung aus der Jensenschen Ungleichung) lässt sich das Ergebnis für beliebige Verteilungen verallgemeinern.
Bitweise Operatoren gehören zu den unterschätzten Werkzeugen in der Programmierung. Wer sie beherrscht, kann Daten kompakter speichern, Informationen blitzschnell verarbeiten und sogar clevere Tricks auf Byte-Ebene anwenden.
In diesem Artikel schauen wir uns an, wie man Daten effizient packt und entpackt, Farbkanäle aus RGB-Werten extrahiert, Flags mit Bitmasken verwaltet – und ganz nebenbei, wie man mit wenigen Zeilen Code Groß- und Kleinschreibung umwandeln kann.
An einfachen Beispielen wird gezeigt, welche Eigenschaften verwendet werden, um eine Markov-Kette zu definieren. Sie stellt eine Verallgemeinerung der unabhängigen Zufallsvariablen dar. Und zwar in dem Sinn, dass in einer Folge von Zufallsvariablen jede Zufallsvariable nur vom Wert der vorhergehenden, nicht aber von noch weiter zurückliegenden Zufallsvariablen abhängt. Die zentrale mathematische Größe zur Beschreibung einer Markov-Kette ist die Übergangsmatrix, welche die Übergangswahrscheinlichkeiten zwischen den möglichen Zuständen (Werten der Zufallsvariablen) festlegt.
Das DRY-Prinzip ("Don't Repeat Yourself") gehört zu den Grundpfeilern wartbarer Softwarearchitektur. In der Praxis wird dieses Prinzip jedoch häufig durchbrochen – insbesondere beim Einsatz von Spring Data Repositories. Wiederkehrende Datenzugriffslogik wie findByStatus oder markAsProcessed taucht oft mehrfach auf, nur leicht variiert für unterschiedliche Entitäten. Ein typisches Beispiel dafür bietet die Implementierung des Outbox-Patterns. Solche Wiederholungen führen schnell zu redundanter, schwer wartbarer Codebasis. Dieser Artikel zeigt, wie sich durch den gezielten Einsatz von @NoRepositoryBean und Spring Expression Language (SpEL) wiederverwendbare Repository-Verträge realisieren lassen – elegant, robust und ganz im Sinne von DRY.
Ist es wirklich ein Hack, wenn man eine Website auf PHP 5.6 zum Absturz bringt? Eigentlich ist das Gegenteil die Kunst: Sie überhaupt noch am Laufen zu halten. 4chan bewies mal wieder: Wer 2025 auf Digital-Archäologie setzt, braucht sich über Einbrüche nicht zu wundern.
Artikel aus dem Jahr 2024
Insgesamt 16, zur Liste aller Artikel aus diesem Jahr.
Tuples gehören in Python zu den wichtigsten Datenstrukturen und finden überall Anwendung, von kleinen bis zu sehr komplexen Projekten.
Sie dienen dazu, mehrere Werte in einer einzigen Variablen zu gruppieren, ähnlich wie Listen.
In diesem Artikel werden wir uns eingehend mit der Syntax, den grundlegenden Funktionen und Operationen
sowie den Einsatzmöglichkeiten von Tupeln beschäftigen.
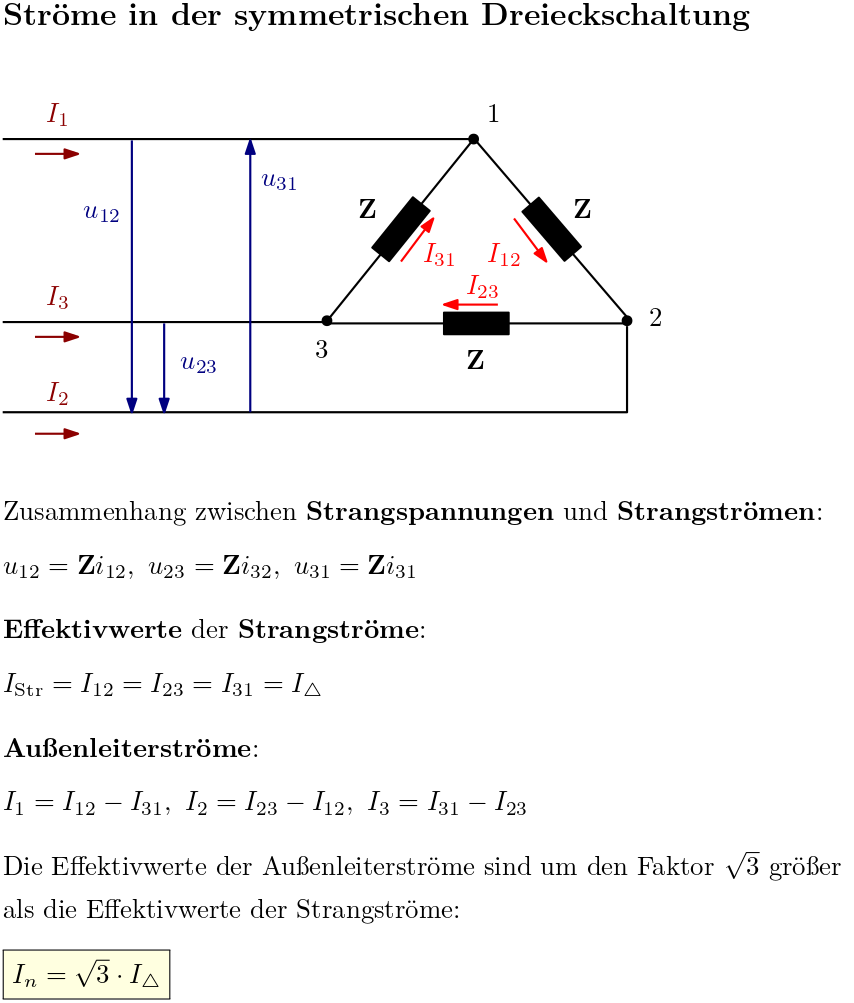
Werden die Verbraucher eines Mehrphasensystems zu einem Ring verkettet, so spricht man im Fall des Dreiphasensystems von der Dreieckschaltung. Diskutiert werden der Aufbau der symmetrischen Dreieckschaltung, die Zusammenhänge zwischen Außenleiterspannung und Strangspannung beziehungsweise Außenleiterstrom und Strangstrom sowie die Berechnung der Leistungen (Wirkleistung, Blindleistung, Scheinleistung).
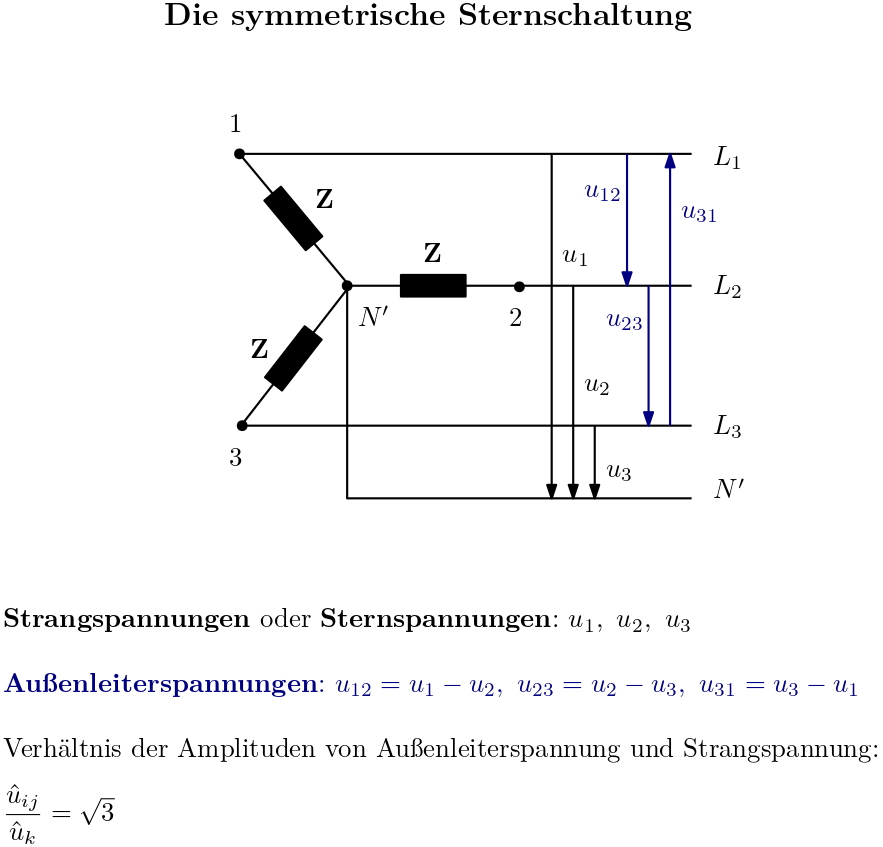
Ein Generator mit gegeneinander verdrehten Wicklungen erzeugt phasenverschobene Spannungen. Diese Spannungen können auf verschiedene Arten eingesetzt werden, um Verbraucher zu versorgen. Eine Möglichkeit besteht darin, sowohl die Spannungsquellen als auch die Verbraucher zu verketten und sie in je einem Sternpunkt zusammenzuführen; die beiden Sternpunkte werden dann leitend miteinander verbunden. Es entsteht die Sternschaltung, die in der Technik mit drei Phasen eingesetzt wird. Die symmetrische Sternschaltung wird entwickelt und die relevanten Leistungen werden berechnet.
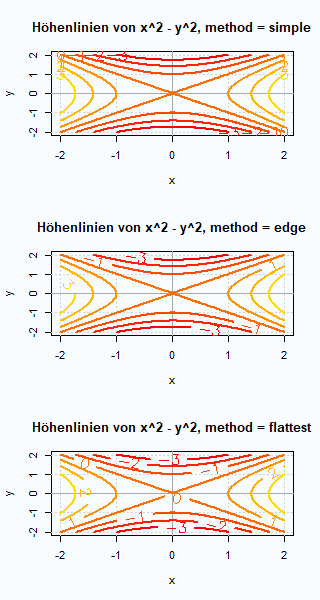
Die Funktion contour() ermöglicht es die Höhenlinien einer reellwertigen Funktion darzustellen, die auf einem zweidimensionalen Gebiet definiert ist. Die Höhenlinien geben manchmal den Graphen besser wieder als eine perspektivische dreidimensionale Darstellung wie sie etwa mit persp() erzeugt werden kann. An einfachen Beispielen werden die Eingabewerte von contour() erläutert.
Pünktlich zu Halloween, wenn Geistergeschichten und gruselige Legenden Hochkonjunktur haben, lohnt es sich, auch in der digitalen Welt nach verborgenen Geheimnissen zu suchen. Der Kauf einer Domain ist oft ein aufregender Schritt auf dem Weg zur eigenen Website, doch was, wenn diese Domain eine düstere Vergangenheit hat? Manche Domains tragen nämlich mehr als nur ihren Namen – sie bringen eine Geschichte voller Spam, Blacklistings oder sogar rechtlicher Probleme mit sich, die wie unsichtbare Geister die neue Website heimsuchen könnten.
Artikel aus dem Jahr 2023
Insgesamt 21, zur Liste aller Artikel aus diesem Jahr.
Akzeptiert man die Entropie als eine Kenngröße einer Wahrscheinlichkeitsverteilung, die die Ungewissheit über den Ausgang eines Zufallsexperimentes beschreibt, so wird man fordern, dass sich bei unabhängigen Zufallsexperimenten die Entropien addieren.
Um diese Aussage schärfer formulieren zu können, wird die gemeinsame Entropie H(X, Y) von zwei Zufallsvariablen eingeführt.
Es wird gezeigt, dass die übliche Definition der Entropie die Additivitätseigenschaft bei unabhängigen Zufallsvariablen X und Y besitzt.
Am Beispiel der isochoren Erwärmung werden die Eigenschaften der freien Energie F = U - TS und der gebundenen Energie G = TS erläutert. Speziell wird gezeigt, wie man ihre Veränderung darstellen kann, wenn man vom US-Diagramm zum TS-Diagramm übergeht.
Die Funktionen substr() und substring() werden eingesetzt, um aus einem String einen Substring zu extrahieren. Dazu müssen die Indizes angegeben werden, wo sich der Substring befindet. In der replacement-Version kann der Substring verändert werden, der Rest des Strings bleibt unverändert. Da die Funktionen vektorisiert sind, kann anstelle einer einzigen Zeichenkette auch ein Vektor von Zeichenketten verarbeitet werden.
Docker-Volumes spielen in Containeranwendungen eine entscheidende Rolle. Sie bieten einen Mechanismus zum Speichern, Verwalten und Zugreifen auf Daten innerhalb von Containern sowie zwischen Containern und dem Host-Computer. Docker-Volumes sind wichtig, um Daten über den Lebenszyklus eines Containers hinaus beizubehalten, Daten zwischen Containern auszutauschen und die Datenintegrität in zustandsbehafteten Anwendungen sicherzustellen.
Unity, ein Unternehmen für Spiele-Engines, hat kürzlich eine Änderung des Lizenzmodells angekündigt, die erhebliche Auswirkungen auf betroffenen Games-Studios haben könnte. Die Reaktionen auf diese Ankündigung fallen eindeutig aus.
Artikel aus dem Jahr 2022
Insgesamt 18, zur Liste aller Artikel aus diesem Jahr.
Die Funktion cat() bietet die einfachste Möglichkeit, Informationen über ein Objekt oder mehrere Objekte auf der Konsole auszugeben. Die Besonderheiten der Funktion werden vorgestellt, wie etwa spezielle Formatierungsanweisungen oder die Möglichkeit die Ausgabe in eine Datei umzuleiten.
Es werden die Wartezeitprobleme bei den beiden Zufallsexperimenten Ziehen mit Zurücklegen beziehungsweise Ziehen ohne Zurücklegen untersucht.
Bei diesen Zufallsexperimenten befinden sich in einer Urne Treffer und Nieten. Mit Wartezeitproblem ist gemeint, dass man eine Zufallsvariable definiert, die angibt nach wie vielen Zügen der r-te Treffer aus der Urne entnommen wird. Zur Vorbereitung werden die Zusammenhänge zwischen Binomialverteilung, geometrischer Verteilung und hyper-geometrischer Verteilung gezeigt.
Dieses Tutorial gibt eine Einführung in die Stringoperationen in Python:
Angefangen mit Zusammenfügen von Zeichenketten, Bestimmen der Länge und das Benutzen des
Index-Operators, um auf einzelne Zeichen zuzugreifen, zeigen wir auch die Iteration über Zeichenketten,
Suchen und Vergleichen von Strings sowie erläutern kurz die Standard-Methoden für Strings in Python.
Das Buch versteht sich als Lernleitfaden zur Verbesserung und Vertiefung der Java-Kenntnisse und bietet dazu eine Sammlung von Übungen und "Programmier Herausforderungen" (daher auch der Titel). Die "Java Challenges" behandeln viele praktische...
Die geometrische Verteilung kann als Verteilung von Wartezeiten aufgefasst werden, wenn man einen Münzwurf solange wiederholt bis der erste Treffer eintritt: man berechnet die Wahrscheinlichkeiten der Anzahl der nötigen Würfe. Man kann dieses Wartezeitproblem verallgemeinern, indem man nicht bis zum ersten sondern bis zum r-ten Treffer wartet. Die Verteilung dieser Wartezeiten wird berechnet und die Eigenschaften der dabei entstehenden Verteilung wird untersucht.
Artikel aus dem Jahr 2021
Insgesamt 23, zur Liste aller Artikel aus diesem Jahr.
Die Definition der Entropie eines Wahrscheinlichkeitsmaßes oder einer Zufallsvariable wird an einfachen Beispielen erläutert. Es wird diskutiert, dass die Entropie kein Streuungsmaß ist (wie die Standardabweichung), sondern die Ungewissheit (oder Unbestimmtheit) des Ausgangs eines Zufallsexperimentes beschreibt.
Die Funktion lm() ist ein mächtiges Instrument für die lineare Regression, das zahlreiche statistische Informationen über die untersuchten Daten bereitstellt. Es wird hier nur für die wichtigsten statistischen Größen gezeigt, wie man sie entweder direkt oder durch weitere Hilfsfunktionen gewinnen kann.
Durch Definition geeigneter Zufallsvariablen (Regressionswert und Residuum) bei einer Regressionsanalyse wird man auf die sogenannte Varianzzerlegung geführt. Sie erlaubt es durch eine einzige Kennzahl (das Bestimmtheitsmaß) zu beurteilen, wie gut die Messdaten durch die Regressionsgerade approximiert werden. Das Diagramm, das die Güte der Approximation am Besten ausdrücken kann, ist der Residualplot.
An zwei konkreten Beispielen wird gezeigt, wie aus stark beziehungsweise schwach korrelierten Messdaten die Regressionsgerade berechnet wird und wie man ihre Eigenschaften veranschaulichen kann. Herleitungen der Formeln zur Berechnung der Regressionskoeffizienten (Methode der kleinsten Quadrate) werden hier nicht gegeben; auch die Quelltexte zur den Berechnungen und Diagrammen werden hier nicht gezeigt.
Geometrische oder dynamische Probleme in drei Dimensionen, die eine Zylindersymmetrie oder Kugelsymmetrie besitzen, lassen sich besonders einfach mit Zylinderkoordinaten beziehungsweise Kugelkoordinaten beschreiben. Diskutiert werden deren Definition, die Koordinatenlinien und -flächen sowie die Basisvektoren. In den R-Skripten werden einige spezielle Eigenschaften näher untersucht und zugleich Beispiele gezeigt, wie dreidimensionale Graphiken mit scatterplot3d erstellt werden.
Artikel aus dem Jahr 2020
Insgesamt 33, zur Liste aller Artikel aus diesem Jahr.
Das Abzählproblem, nicht unterscheidbare Kugeln auf nicht unterscheidbare Urnen zu verteilen ist äquivalent zum Problem zu einer ganzen Zahl Z Zerlegung in L Summanden zu finden. Eine derartige Zerlegung wird als Partition bezeichnet. Wie viele Partitionen es gibt, wird für mehrere Fälle untersucht: Die Vertauschung der Reihenfolge zählt (oder zählt nicht) als neue Partition, die Null ist als Summand zugelassen, die Länge der Partition wird nicht festgelegt. Man kann für diese Abzählprobleme zwar Rekursionsformeln angeben, man kann mit einfachen Mitteln aber keine expliziten Formeln angeben, die die Rekursionsformeln lösen.
Kombinationen mit Wiederholungen treten in mehreren Abzählproblemen auf, die zunächst sehr unterschiedlich wirken. Es wird ihre Äquivalenz gezeigt und die Formel hergeleitet, wie man die Anzahl aller Kombinationen mit Wiederholungen berechnet. Dazu verwendet man die Methode Stars and Bars. In den R-Skripten wird ein einfacher Algorithmus gezeigt, wie man die Menge alle Kombinationen mit Wiederholungen rekursiv berechnet.
Die Funktion sample() wird verwendet, um Stichproben zu erzeugen. Sie lässt sich so konfigurieren, dass man die Wahrscheinlichkeitsverteilungen von beliebigen selbstdefinierten diskreten Zufallsvariablen einsetzen kann. Zudem kann man das Ziehen mit beziehungsweise ohne Zurücklegen realisieren.
Mit Hilfe von Zeigern kann man Funktionen realisieren, die Felder als Eingabewert beziehungsweise als Rückgabewert besitzen. Es ist sogar möglich, Zeiger auf Funktionen zu setzen und damit Funktionen als Eingabewerte anderer Funktionen einzusetzen.
Es werden einfache Aufgaben besprochen, die grundlegende Eigenschaften von Feldern und Zeigern behandeln und die man nach einem ersten Durchgang durch diese Themen beherrschen sollte.
Artikel aus dem Jahr 2019
Insgesamt 54, zur Liste aller Artikel aus diesem Jahr.
Programmieraufgaben zur Anwendung von Feldern und Zeigern, die im Sinne der strukturierten Programmierung zu lösen sind. Die Quelltexte sollen in reinem C geschrieben werden, also keine Konzepte verwenden, die nur in C++ verfügbar sind.
Was zeichnet das Buch aus? Die Entdeckungsreise von Matoušek und Nešetřil will so gar nicht in die üblichen Kategorien von Mathematik-Büchern passen: Es gibt Lehrbücher, die streng nach dem Prinzip Definition – Satz – Beweis aufgebaut sind und die den Leser meist mit der Frage zurücklassen: "Wie soll ich jemals derartige Mathematik selber machen?" Und es gibt populärwissenschaftliche Bücher, die viel zu oberflächlich sind, um mit ihnen eigene mathematische Fähigkeiten entwickeln zu können. Warum ordnet sich die Entdeckungsreise hier nicht ein? Einerseits enthält es Definitionen, Sätze und Beweise und ein Blick in das Inhaltsverzeichnis erweckt den Eindruck eines üblichen Lehrbuches, andererseits findet man beim zufälligen Aufschlagen immer wieder Passagen im Plauderton . Dennoch ist es alles andere als eine Mischung der beiden genannten Kategorien. Um dies festzustellen, reicht es ein Kapitel zu lesen, von dem man glaubt, es schon gut zu kennen – selbst dort wird man...
Felder werden durch Zeiger organisiert und es ist gerade ein Charakteristikum der Sprache C, dass dies nicht nur intern verwendet wird, sondern dass man diesen Mechanismus selbst nutzen kann. Für den Einsteiger ist dies meist mit Schwierigkeiten verbunden, da man oft nicht entscheiden kann, mit welchem Objekt man gerade arbeitet (Zeiger oder Variable eines fundamentalen Datentyps). Die meisten der mit Feldern verbundenen Schwierigkeiten wie etwa die Zeigerarithmetik, die Ausgabe und der Vergleich von Feldern werden erklärt. Wie man Felder an Funktionen übergibt oder als Rückgabewert zurückerhält, wird im nächsten Kapitel erläutert.
In einem Feld werden mehrer Komponenten von gleichem Datentyp zu einem Objekt zusammengefasst. Die Anzahl der Komponenten muss bei der Deklaration angegeben werden und darf sich während der Laufzeit des Programmes nicht ändern. Der häufigste Fehler beim Umgang mit Feldern besteht im Zugriff auf Komponenten jenseits des deklarierten Bereichs, was zu unbestimmtem Verhalten des Programmes führen kann. Die unterschiedlichen Möglichkeiten zur Initialisierung eines Feldes werden vorgestellt. Felder können in beliebig vielen Dimensionen angelegt werden; besprochen werden hier nur eindimensionale Felder (Vektoren) und zweidimensionale Felder (Matrizen).
Zeiger sind Variable, deren Wert eine Adresse ist. Man kann sie mit der Adresse einer anderen Variable initialisieren. Da unterschiedliche Datentypen unterschiedlich großen Speicherplatz belegen, muss bei der Deklaration eines Zeigers angegeben werden, welchen Datentyp die Variable besitzt, auf deren Speicherplatz er verweist. Diese Eigenschaften von Zeigern und mit welchen Operatoren (Adressoperator, Indirektionsoperator) dies realisiert wird, wird hier ausführlich diskutiert. Als Anwendung wird gezeigt, wie man mit Zeigern Funktionen realisieren kann, die mehrere Rückgabewerte besitzen.
Artikel aus dem Jahr 2018
Insgesamt 54, zur Liste aller Artikel aus diesem Jahr.
Felder sind in R die Verallgemeinerung von Matrizen. In einer Matrix werden die Komponenten zweidimensional angeordnet (Zeilen und Spalten), in einem Feld sind beliebige Dimensionen zugelassen. Erzeugt werden Felder meist, indem ein Vektor mit Hilfe des Dimensionsvektors mehrdimensional angeordnet wird, oder mit der Funktion outer(). Weitere Gemeinsamkeiten und Unterschiede zu Matrizen werden diskutiert.
Vorgestellt wird, wie Matrizen miteinander verknüpft werden, welche Funktionen Eigenschaften von Matrizen anzeigen, sowie zahlreiche Funktionen aus der Linearen Algebra (Berechnung von Determinanten, Lösung von linearen Gleichungssystemen, Berechnung von transponierten und inversen Matrizen, Berechnung von Eigenwerten und Eigenvektoren).
Die Komponenten eines Vektors können in R zweidimensional angeordnet werden wie in einer Matrix. Es werden verschiedene Möglichkeiten gezeigt, wie man Matrizen erzeugen kann, wie man spezielle Matrizen erzeugt und wie man auf die Komponenten einer Matrix zugreift. Weiter werden der Dimensionsvektor (Attribut dim) und das optionale Attribut dimnames vorgestellt. Wie Matrizen verknüpft werden und weitere Anwendungen folgen im nächsten Kapitel (Matrizen in R: Anwendungen).
Grundlegend für das Verständnis von Operationen, die mit Vektoren ausgeführt werden können, sind die punktweise Ausführung (eine Operation wird an die Komponenten weitergereicht) und der recycling-Mechanismus, der festlegt, wie Vektoren mit unterschiedlichen Längen verknüpft werden. Ausgehend hiervon werden zahlreiche Operationen vorgestellt, die mit Vektoren ausgeführt werden können (wie zum Beispiel statistische Funktionen, Sortier-Algorithmen, Mengen-Operationen).
Da es in R eigentlich keine fundamentalen Datentypen gibt (wie ganze Zahlen, Gleitkommazahlen, Zeichen, logische Werte), sondern diese Spezialfall eines Vektors der Länge 1 sind, ist dieses Kapitel entscheidend für das Verständnis von R. Vektoren bestehen aus Komponenten mit identischem Speichermodus und die Komponenten sind numeriert (oder wie man auch sagt: indiziert).
Vorgestellt werden hier Funktionen zum Erzeugen von Vektoren, der Zugriff auf die Komponenten eines Vektors, Diagnose-Funktionen für Vektoren und das Attribut names. Wie man Vektoren verknüpft und welche weiteren Funktionen zur Weiterverarbeitung von Vektoren existieren, wird im nächsten Kapitel gezeigt (Vektoren in R: Anwendungen).
Artikel aus dem Jahr 2017
Insgesamt 14, zur Liste aller Artikel aus diesem Jahr.
Inhaltsverzeichnis und Lernziele des Kapitels C++: Fortgeschrittene Syntax.
Inhalt und Lernziele des Kapitels Einführung in C++.
Einige einfache arithmetische Operationen können in C++ in einer Kurzform geschrieben werden (Inkrement-Operator, Dekrement-Operator, Kurzform-Operatoren).
Wenn möglich sollen diese auch eingesetzt werden, da sie schneller ausgeführt werden als die entsprechenden Befehle in der ausführlichen Schreibweise.
Die Aufgaben des Betriebssystems werden genannt und Prozess-Management und Speichermanagement näher erläutert.
Außer den allseits bekannten Notebooks und PCs gibt es eine Vielzahl von Computersystemen mit unterschiedlicher Leistungsfähigkeit in vielfältigen Anwendungsgebieten.
Die wichtigsten dieser Computersysteme werden hier kurz vorgestellt.