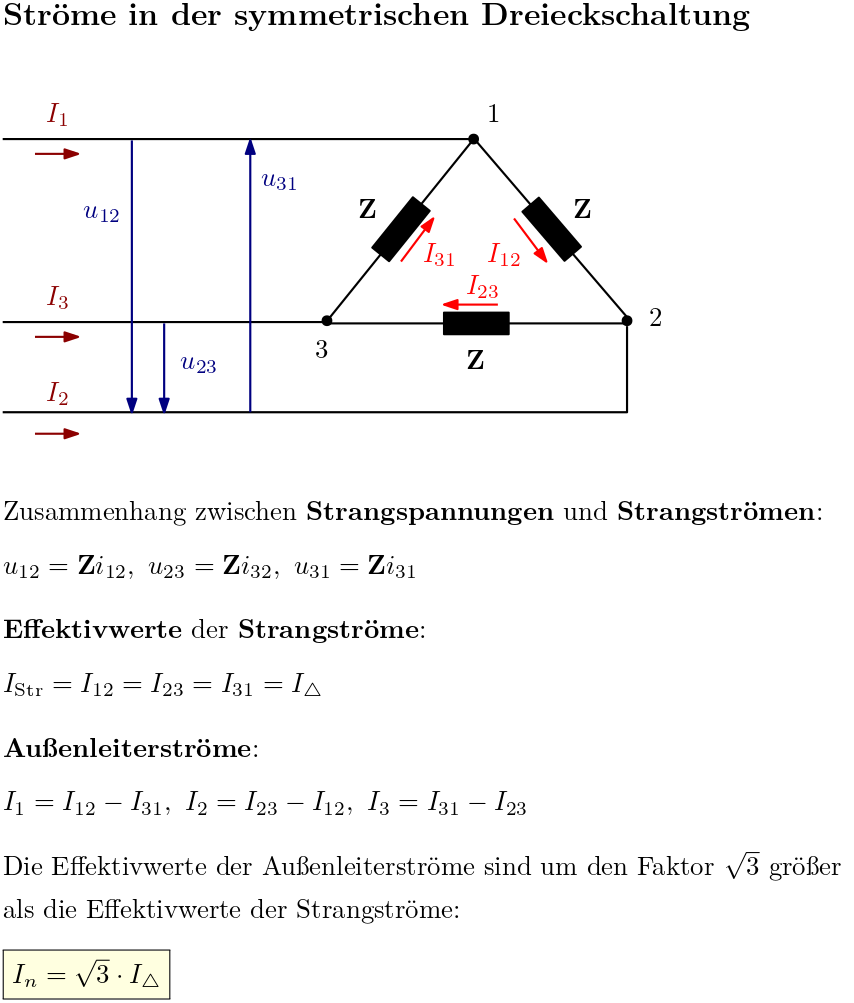
Werden die Verbraucher eines Mehrphasensystems zu einem Ring verkettet, so spricht man im Fall des Dreiphasensystems von der Dreieckschaltung. Diskutiert werden der Aufbau der symmetrischen Dreieckschaltung, die Zusammenhänge zwischen Außenleiterspannung und Strangspannung beziehungsweise Außenleiterstrom und Strangstrom sowie die Berechnung der Leistungen (Wirkleistung, Blindleistung, Scheinleistung).
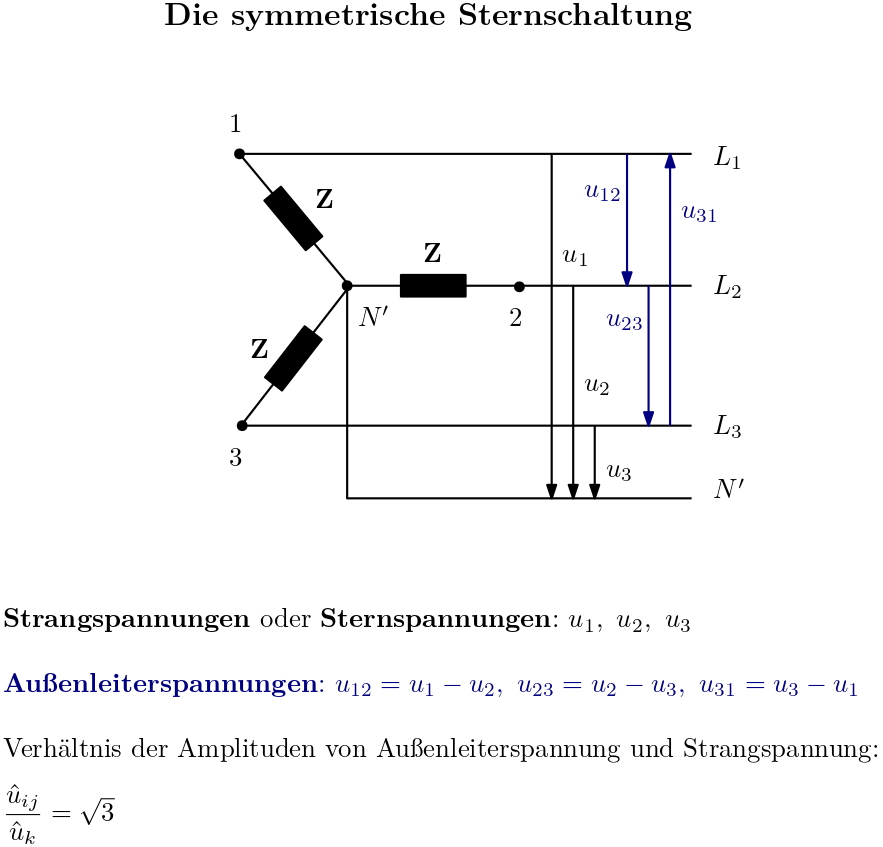
Ein Generator mit gegeneinander verdrehten Wicklungen erzeugt phasenverschobene Spannungen. Diese Spannungen können auf verschiedene Arten eingesetzt werden, um Verbraucher zu versorgen. Eine Möglichkeit besteht darin, sowohl die Spannungsquellen als auch die Verbraucher zu verketten und sie in je einem Sternpunkt zusammenzuführen; die beiden Sternpunkte werden dann leitend miteinander verbunden. Es entsteht die Sternschaltung, die in der Technik mit drei Phasen eingesetzt wird. Die symmetrische Sternschaltung wird entwickelt und die relevanten Leistungen werden berechnet.
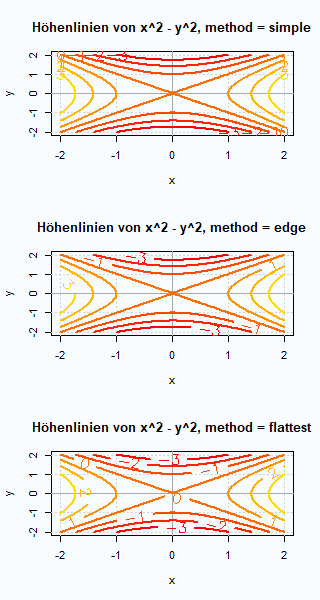
Die Funktion contour() ermöglicht es die Höhenlinien einer reellwertigen Funktion darzustellen, die auf einem zweidimensionalen Gebiet definiert ist. Die Höhenlinien geben manchmal den Graphen besser wieder als eine perspektivische dreidimensionale Darstellung wie sie etwa mit persp() erzeugt werden kann. An einfachen Beispielen werden die Eingabewerte von contour() erläutert.
Pünktlich zu Halloween, wenn Geistergeschichten und gruselige Legenden Hochkonjunktur haben, lohnt es sich, auch in der digitalen Welt nach verborgenen Geheimnissen zu suchen. Der Kauf einer Domain ist oft ein aufregender Schritt auf dem Weg zur eigenen Website, doch was, wenn diese Domain eine düstere Vergangenheit hat? Manche Domains tragen nämlich mehr als nur ihren Namen – sie bringen eine Geschichte voller Spam, Blacklistings oder sogar rechtlicher Probleme mit sich, die wie unsichtbare Geister die neue Website heimsuchen könnten.
Primitive Datentypen sind die Grundlage für Datenverarbeitung und -speicherung in Java, da sie einfache Werte effizient und ohne den Overhead von Objekten speichern. Dieser Artikel bietet eine Einführung in die grundlegenden Eigenschaften jedes primitiven Datentyps und erläutert Speicherbedarf sowie Wertebereiche.
Das Mono-Projekt hat überraschend die Verwaltung an WineHQ übergeben, was eine wichtige Phase im .NET-Ökosystem abschließt. Dieser Schritt hat Diskussionen über Monos Erbe und zukünftige Entwicklung angestoßen.
Bereit für das ultimative Textabenteuer? Mit Vim-Racer.com kannst du nicht nur deine Navigationskünste in Vim auf die Probe stellen, sondern dich auch in einem rasanten Wettkampf gegen andere Entwickler beweisen. Schalte den Turbo ein, fliege durch den Code und zeige, dass du der Schnellste auf der Tastatur bist – alles ganz ohne Fingerkrämpfe oder Emacs-Verirrungen!
In diesem Artikel werden wir vier verschiedene Methoden zur Listenfilterung in Python untersuchen: Iteration, die filter-Funktion, List Comprehension und die itertools-Bibliothek. Jede Methode hat ihre eigenen Stärken und Schwächen, wodurch sie für unterschiedliche Szenarien und Anwendungsfälle geeignet sind.
Convolutional Neural Networks (CNNs) sind eine der grundlegendsten und leistungsstärksten Methoden in der modernen Computer Vision. Sie ermöglichen es Computern, spezifische Objekte in zweidimensionalen Bildern zu erkennen und haben Anwendungen in Bereichen wie Bildklassifizierung, Objekterkennung und Gesichtserkennung revolutioniert. In diesem Artikel werden wir die grundlegenden Konzepte eines CNNs kennenlernen und anhand eines einfachen Beispiels demonstrieren, wie man ein eigenes CNN erstellen kann.
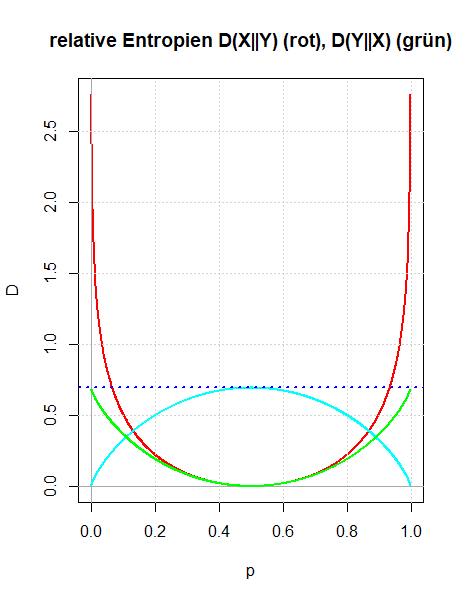
Es werden zwei Zugänge gezeigt, wie man die relative Entropie motivieren kann: Entweder als Verallgemeinerung der gegenseitigen Information oder indem man die Überlegungen Boltzmanns zur Definition der Entropie in dem Sinn verallgemeinert, dass man die Voraussetzung der Gleichwahrscheinlichkeit der Mikrozustände aufgibt. Die Bedeutung der relativen Entropie als einer Größe, die quantifiziert, wie unterschiedlich zwei Wahrscheinlichkeitsverteilungen sind, wird durch den zweiten Zugang besser verständlich.
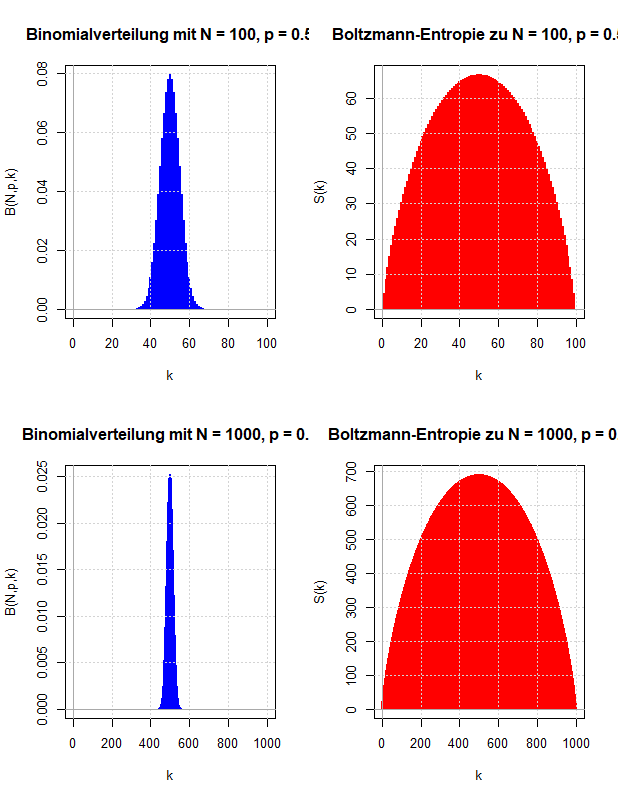
Ludwig Boltzmann gab eine mikroskopische Erklärung für die thermodynamische Entropie, die nach dem zweiten Hauptsatz der Thermodynamik niemals abnehmen kann. Diese Überlegungen werden verwendet, um zu motivieren, wie die Entropie der Wahrscheinlichkeitstheorie definiert wird, die die Ungewissheit über den Wert einer Zufallsvariable quantifizieren soll.
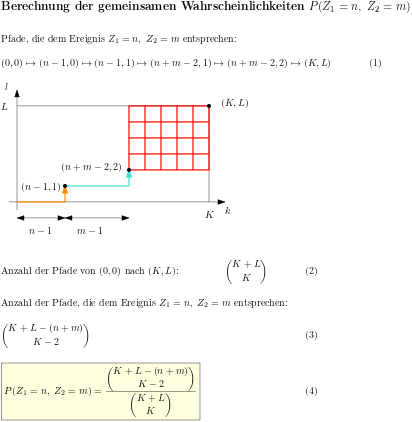
Die Entropie einer Zufallsvariable, die gemeinsame Entropie zweier Zufallsvariablen und die gegenseitige Information werden am Beispiel der Wartezeitprobleme beim Ziehen ohne Zurücklegen veranschaulicht. Dazu werden als Zufallsvariablen die Wartezeit bis zum ersten Treffer und die Wartezeit vom ersten bis zum zweiten Treffer verwendet.
YAML ("YAML Ain't Markup Language", mißverständlich auch "yet another markup language") ist eine Datenformatsprache, die in einer Vielzahl von Anwendungen eingesetzt wird, darunter die Konfiguration von Continuous Integration / Continuous Deployment (CI/CD) Pipelines, Docker- und Kubernetes-Konfigurationen sowie andere Softwareanwendungen. In diesem Artikel zeigen wir die Verwendung von SnakeYAML mit Java, einer leistungsstarken Bibliothek, die das Laden von YAML-Dateien als Map oder direkt in benutzerdefinierte Typen (POJOs) ermöglicht.
Überträgt man den Begriff der Entropie einer Zufallsvariable auf die Wahrscheinlichkeitsverteilungen von zwei Zufallsvariablen, so ist es naheliegend die gemeinsame Entropie und die bedingte Entropie einzuführen, die über die Kettenregel miteinander verknüpft sind. Diese wiederum motiviert die Einführung einer neuen Größe, der gegenseitigen Information zweier Zufallsvariablen. Sie ist symmetrisch in den beiden Zufallsvariablen und beschreibt die Information, die in einer Zufallsvariable über die andere Zufallsvariable enthalten ist. An einfachen Beispielen wird die Definition der gegenseitigen Information motiviert und veranschaulicht.
Die Entropie wurde eingeführt als ein Maß für die Ungewissheit über den Ausgang eines Zufallsexperimentes. Entsprechend kann man eine bedingte Entropie definieren, wenn man die bedingten Wahrscheinlichkeiten verwendet, wobei man als Bedingung entweder ein Ereignis oder eine Zufallsvariable zulässt. Die Definition der bedingten Entropie und ihr Zusammenhang mit der gemeinsamen Entropie zweier Zufallsvariablen (Kettenregel) wird an einfachen Beispielen erläutert.
