geometrische Verteilung
Die geometrische Verteilung ist eine spezielle Wahrscheinlichkeitsverteilung, die in der Wahrscheinlichkeitsrechnung und Statistik verwendet wird. Sie beschreibt die Anzahl der Versuche, die benötigt werden, um das erste Erfolgsergebnis in einem stochastischen Experiment zu erzielen.
Bei der geometrischen Verteilung handelt es sich um eine diskrete Verteilung, da die Anzahl der Versuche nur ganze Zahlen sein kann. Sie wird oft verwendet, um Wartezeitprobleme zu lösen, bei denen man beispielsweise wissen möchte, wie viele Versuche benötigt werden, um eine bestimmte Anzahl an Erfolgen zu erzielen.
Der Erwartungswert einer geometrischen Verteilung gibt die durchschnittliche Anzahl der Versuche an, die benötigt werden, um den ersten Erfolg zu erzielen. Die Varianz und die Standardabweichung geben an, wie stark die Anzahl der Versuche um den Erwartungswert streut.
In einem unserer Artikel haben wir bereits die Grundbegriffe der Wahrscheinlichkeitsrechnung und die Eigenschaften von Zufallsvariablen behandelt. Dort haben wir auch den Erwartungswert und die Varianz von diskreten und stetigen Zufallsvariablen besprochen.
Die geometrische Verteilung kann auch verwendet werden, um Wartezeitprobleme beim Ziehen mit Zurücklegen oder Ziehen ohne Zurücklegen zu lösen. Dabei interessiert man sich beispielsweise dafür, wie viele Versuche benötigt werden, um eine bestimmte Anzahl an Erfolgen zu erzielen, wenn man immer wieder Kugeln aus einer Urne zieht.
Eine weitere spezielle Wahrscheinlichkeitsverteilung, die in ähnlichen Kontexten verwendet wird, ist die hypergeometrische Verteilung. Sie beschreibt die Anzahl der Erfolge in einer Stichprobe ohne Zurücklegen.
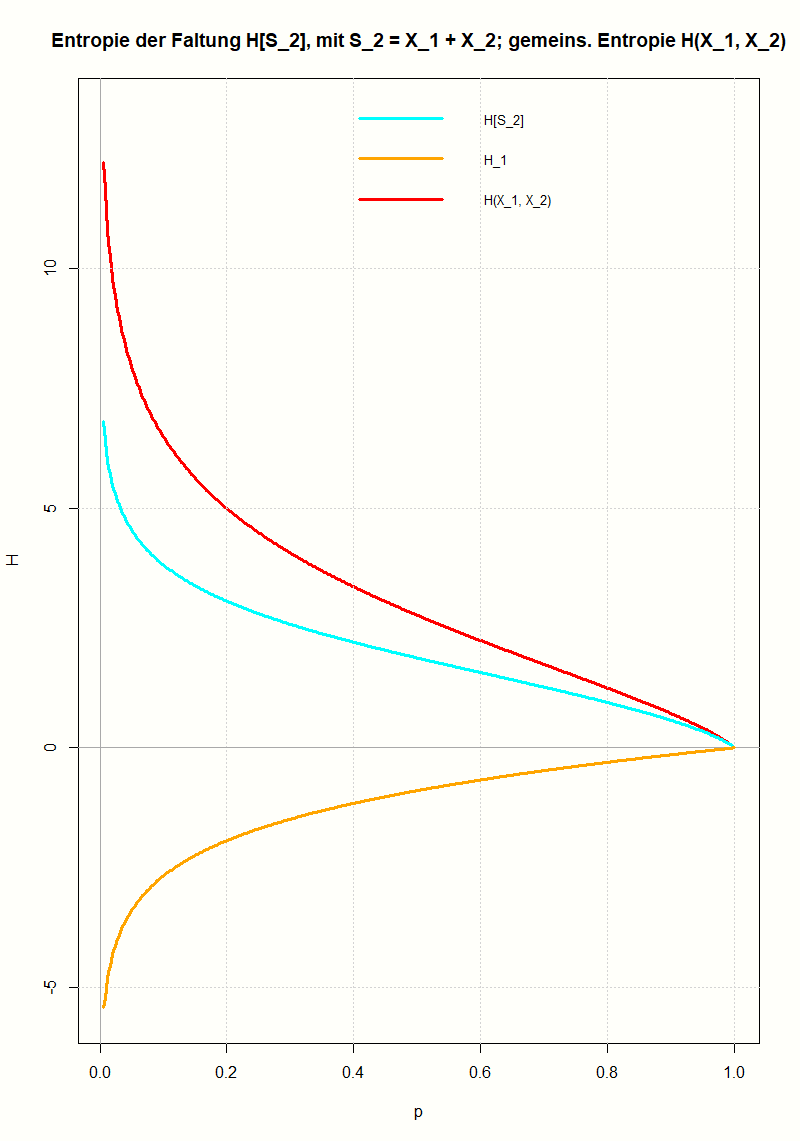
Am Beispiel der geometrischen Verteilung wird gezeigt, wie man die Entropie einer Faltung berechnet und wie sie mit den Entropien der Ausgangsverteilungen zusammenhängt. Mit Hilfe der Log-Summen-Ungleichung (einer Folgerung aus der Jensenschen Ungleichung) lässt sich das Ergebnis für beliebige Verteilungen verallgemeinern.
Die Entropie einer Zufallsvariable, die gemeinsame Entropie zweier Zufallsvariablen und die gegenseitige Information werden am Beispiel der Wartezeitprobleme beim Ziehen ohne Zurücklegen veranschaulicht. Dazu werden als Zufallsvariablen die Wartezeit bis zum ersten Treffer und die Wartezeit vom ersten bis zum zweiten Treffer verwendet.
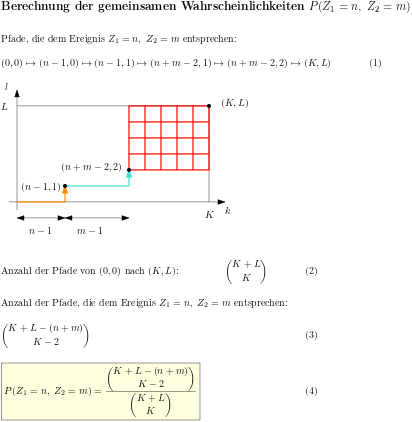
Die Zufallsexperimente Ziehen mit Zurücklegen beziehungsweise Ziehen ohne Zurücklegen werden umformuliert in eine Zufallsbewegung auf einem Gitter. Dadurch lassen sich viele Herleitungen besser veranschaulichen. Gezeigt wird dies hier für die Verteilungen der Zufallsvariablen, die die Anzahl der Treffer oder die Wartezeit bis zu einem bestimmten Treffer beschreiben.
Es werden die Wartezeitprobleme bei den beiden Zufallsexperimenten Ziehen mit Zurücklegen beziehungsweise Ziehen ohne Zurücklegen untersucht.
Bei diesen Zufallsexperimenten befinden sich in einer Urne Treffer und Nieten. Mit Wartezeitproblem ist gemeint, dass man eine Zufallsvariable definiert, die angibt nach wie vielen Zügen der r-te Treffer aus der Urne entnommen wird. Zur Vorbereitung werden die Zusammenhänge zwischen Binomialverteilung, geometrischer Verteilung und hyper-geometrischer Verteilung gezeigt.
Die geometrische Verteilung kann als Verteilung von Wartezeiten aufgefasst werden, wenn man einen Münzwurf solange wiederholt bis der erste Treffer eintritt: man berechnet die Wahrscheinlichkeiten der Anzahl der nötigen Würfe. Man kann dieses Wartezeitproblem verallgemeinern, indem man nicht bis zum ersten sondern bis zum r-ten Treffer wartet. Die Verteilung dieser Wartezeiten wird berechnet und die Eigenschaften der dabei entstehenden Verteilung wird untersucht.
Für das Modellsystem mit unabhängigen Teilchen, die äquidistante Energieniveaus besitzen, werden die wichtigsten statistischen und thermodynamischen Größen berechnet.
Die geometrische Verteilung wird verwendet, um Wartezeiten zu modellieren. Die grundlegenden Eigenschaften wie Erwartungswert, Varianz, Standardabweichung, die Verteilungsfunktion und insbesondere der Zusammenhang zur Binomialverteilung und die sogenannte Gedächtnislosigkeit werden besprochen.
Nach dem Erwartungswert sind die Varianz und die Standardabweichung (als Wurzel der Varianz) die wichtigsten Kennzahlen einer Verteilung. Ist der Erwartungswert ein Maß für die Lage der Verteilung, beschreiben Varianz und Standardabweichung die Streuung der Werte einer Zufallsvariable um den Erwartungswert. Die Definition und Eigenschaften werden besprochen und an zahlreichen Beispielen erläutert.
Der Erwartungswert einer Zufallsvariable ist die wichtigste Kennzahl, um Ergebnisse von Zufallsexperimenten zu beschreiben. Seine Definition und Eigenschaften werden ausführlich erläutert. An zahlreichen Beispielen wird seine Berechnung vorgeführt; dabei werden nebenbei wichtige Wahrscheinlichkeits-Verteilungen vorgestellt.
Zufallsvariablen können diskrete oder kontinuierliche Werte annehmen. Die mathematische Beschreibung unterscheidet sich, da die Wahrscheinlichkeiten der Werte der Zufallsvariable entweder mit Folgen oder indirekt über eine Wahrscheinlichkeitsdichte angegeben werden. Diese Beschreibung wird an speziellen Verteilungen demonstriert: diskrete Gleichverteilung, Poisson-Verteilung, kontinuierliche Gleichverteilung, Standard-Normalverteilung.
Die fundamentalen Begriffe der Wahrscheinlichkeitsrechnung, nämlich Ereignisalgebra, Wahrscheinlichkeit, Wahrscheinlichkeitsraum und die Axiome von Kolmogorov, werden formuliert. Es werden einige einfache Anwendungen und Skripte für Simulationen von Zufallsexperimenten gezeigt.