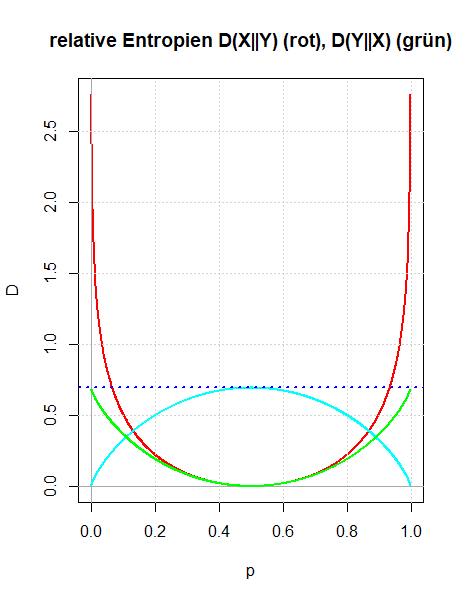
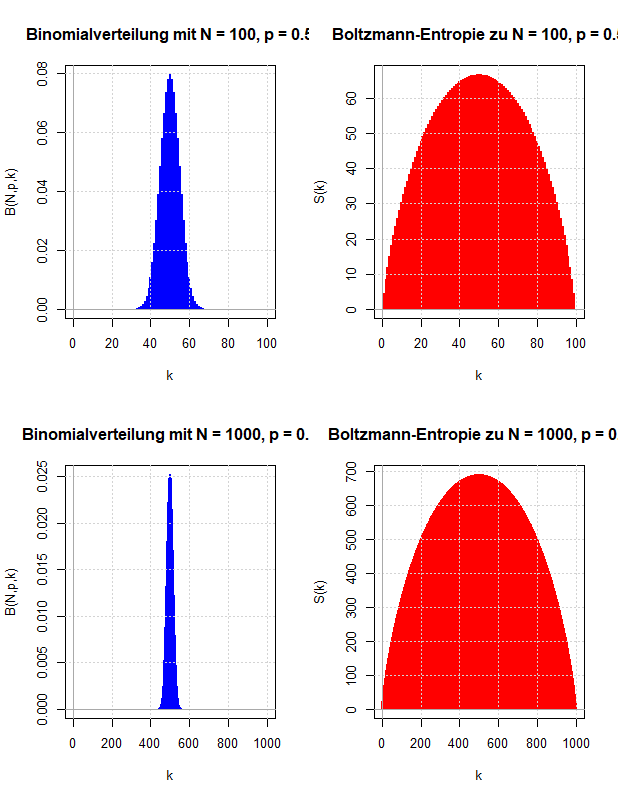
Es werden zwei Zugänge gezeigt, wie man die relative Entropie motivieren kann: Entweder als Verallgemeinerung der gegenseitigen Information oder indem man die Überlegungen Boltzmanns zur Definition der Entropie in dem Sinn verallgemeinert, dass man die Voraussetzung der Gleichwahrscheinlichkeit der Mikrozustände aufgibt. Die Bedeutung der relativen Entropie als einer Größe, die quantifiziert, wie unterschiedlich zwei Wahrscheinlichkeitsverteilungen sind, wird durch den zweiten Zugang besser verständlich.
Ludwig Boltzmann gab eine mikroskopische Erklärung für die thermodynamische Entropie, die nach dem zweiten Hauptsatz der Thermodynamik niemals abnehmen kann. Diese Überlegungen werden verwendet, um zu motivieren, wie die Entropie der Wahrscheinlichkeitstheorie definiert wird, die die Ungewissheit über den Wert einer Zufallsvariable quantifizieren soll.
Die Zufallsexperimente Ziehen mit Zurücklegen beziehungsweise Ziehen ohne Zurücklegen werden umformuliert in eine Zufallsbewegung auf einem Gitter. Dadurch lassen sich viele Herleitungen besser veranschaulichen. Gezeigt wird dies hier für die Verteilungen der Zufallsvariablen, die die Anzahl der Treffer oder die Wartezeit bis zu einem bestimmten Treffer beschreiben.
Die Faltung von Wahrscheinlichkeitsmaßen ist eine der wichtigsten Begriffsbildungen, um Summen von unabhängigen Zufallsvariablen zu beschreiben, da sich mit ihr viele Eigenschaften von Zufallsvariablen und Wahrscheinlichkeitsverteilungen prägnant formulieren lassen und zahlreiche Bezüge zu anderen (scheinbar entfernten) Begriffen und Aussagen herstellen lassen. In diesem einführenden Kapitel wird auf exakte mathematische Definitionen und Beweise verzichtet, stattdessen soll der Begriff der Faltung an typischen Beispielen motiviert werden.
Die Herleitung der Chernoff-Schranke beruht auf der momentenerzeugenden Funktion. Für den Spezialfall der Binomialverteilung kann die optimale Chernoff-Schranke explizit berechnet werden und es geht außer der Markov-Ungleichung keine weitere Näherung ein. Um die Vorgehensweise bei der Berechnung der Chernoff-Schranke besser verständlich zu machen, werden alle Herleitungsschritte besprochen und mit zahlreichen Diagrammen veranschaulicht.
Zu den wichtigsten Wahrscheinlichkeitsverteilungen gibt es Funktionen zum Berechnen der Wahrscheinlichkeitsdichte, der Verteilungsfunktion, des p-Quantils und zum Erzeugen von Zufallszahlen. Für ausgewählte Verteilungen (Binomialverteilung, Poisson-Verteilung, kontinuierliche Gleichverteilung und Normalverteilung) werden diese Funktionen vorgestellt. Dabei werden typische Anwendungen aus der Wahrscheinlichkeitsrechnung und Statistik gezeigt, die zugleich einige Eigenschaften dieser Verteilungen illustrieren.