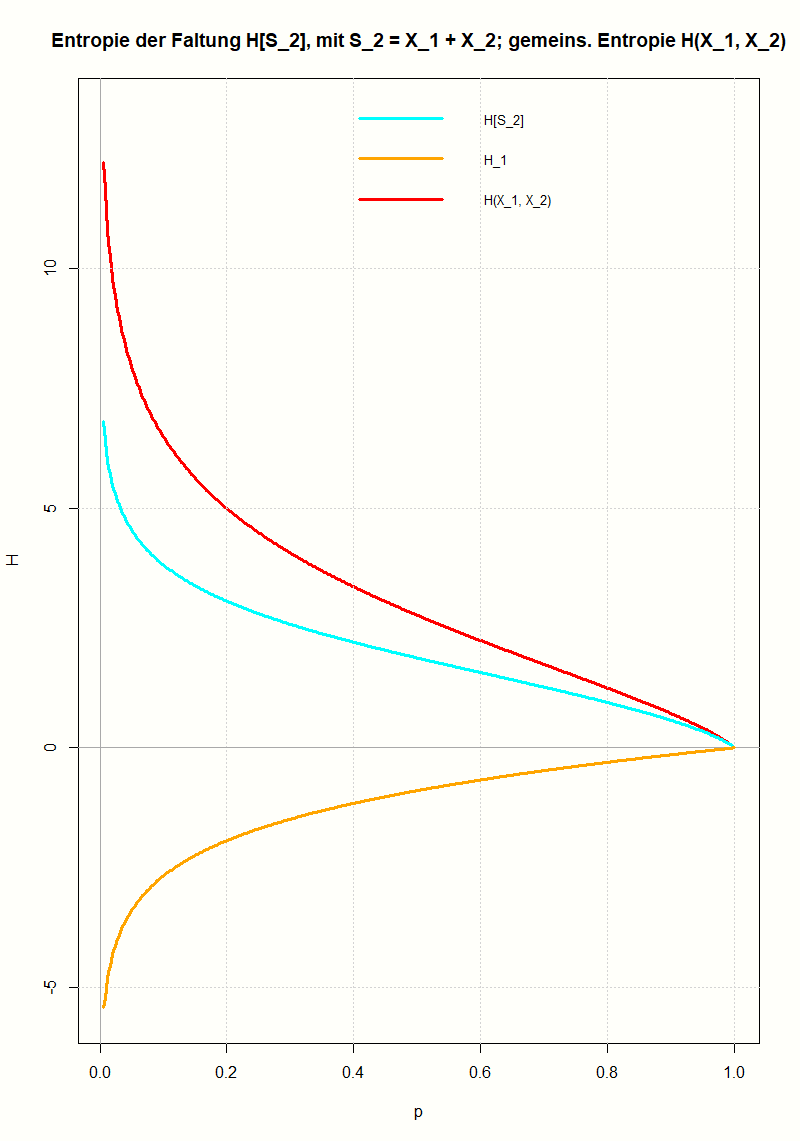
Am Beispiel der geometrischen Verteilung wird gezeigt, wie man die Entropie einer Faltung berechnet und wie sie mit den Entropien der Ausgangsverteilungen zusammenhängt. Mit Hilfe der Log-Summen-Ungleichung (einer Folgerung aus der Jensenschen Ungleichung) lässt sich das Ergebnis für beliebige Verteilungen verallgemeinern.
In den vorausgegangenen Kapiteln wurden die Abzählprobleme behandelt, die sich ergeben, wenn ein thermodynamisches System entweder auf der Ebene der Mikrozustände oder der Makrozustände beschrieben wird. Vergleicht man diese Ergebnisse mit den Gleichungen der phänomenologischen Thermodynamik, kann man eine statistische Definition der Entropie ableiten und damit eine (statistische) Erklärung des zweiten Hauptsatzes der Thermodynamik liefern. Die Boltzmann-Entropie wird mit Hilfe der Anzahl der Mikrozustände pro Makrozustand definiert und besitzt die Eigenschaften, die man innerhalb der Thermodynamik an die Entropie stellt.
Zufallsvariablen sind die geeignete Begriffsbildung um sowohl Ereignisse als auch deren Wahrscheinlichkeiten treffend zu beschreiben und zu berechnen. In späteren Anwendungen der Wahrscheinlichkeitsrechnung werden Zufallsvariablen ständig eingesetzt. Hier wird zunächst gezeigt, wie Zufallsvariablen mit der Ereignisalgebra und dem Wahrscheinlichkeitsmaß zusammenhängen und sich so nahtlos in den Aufbau der Wahrscheinlichkeitsrechnung einfügen. In den R-Skripten wird gezeigt, wie man Zufallsvariable leicht modellieren kann.
In der Statistik muss man oft Daten gruppieren und die gruppierten Daten auswerten. In R wird eine derartige Gruppierung mit einem Faktor (oder mehreren Faktoren) vorgenommen. Das Kapitel beschreibt R-Funktionen, die diese Aufgaben erleichtern, und zeigt ihre praktische Anwendung.