Die Entropie einer Zufallsvariable, die gemeinsame Entropie zweier Zufallsvariablen und die gegenseitige Information werden am Beispiel der Wartezeitprobleme beim Ziehen ohne Zurücklegen veranschaulicht. Dazu werden als Zufallsvariablen die Wartezeit bis zum ersten Treffer und die Wartezeit vom ersten bis zum zweiten Treffer verwendet.
Die Zufallsexperimente Ziehen mit Zurücklegen beziehungsweise Ziehen ohne Zurücklegen werden umformuliert in eine Zufallsbewegung auf einem Gitter. Dadurch lassen sich viele Herleitungen besser veranschaulichen. Gezeigt wird dies hier für die Verteilungen der Zufallsvariablen, die die Anzahl der Treffer oder die Wartezeit bis zu einem bestimmten Treffer beschreiben.
Es werden die Wartezeitprobleme bei den beiden Zufallsexperimenten Ziehen mit Zurücklegen beziehungsweise Ziehen ohne Zurücklegen untersucht.
Bei diesen Zufallsexperimenten befinden sich in einer Urne Treffer und Nieten. Mit Wartezeitproblem ist gemeint, dass man eine Zufallsvariable definiert, die angibt nach wie vielen Zügen der r-te Treffer aus der Urne entnommen wird. Zur Vorbereitung werden die Zusammenhänge zwischen Binomialverteilung, geometrischer Verteilung und hyper-geometrischer Verteilung gezeigt.
Die Methode, den Erwartungswert einer Zufallsvariable X mit Hilfe von Indikatorvariablen zu berechnen, ist deshalb so wichtig, weil man dazu die Verteilung von X nicht kennen muss. Die eigentliche Schwierigkeit besteht oft darin, geeignete Indikatorvariablen zu finden. An mehreren Beispielen (Münzwurf, hypergeometrische Verteilung und einer Zufallsvariable mit unbekannter Verteilung) wird dieses Vorgehen demonstriert. Da man Varianzen auf Erwartungswerte zurückführen kann, lassen sich mit dieser Methode auch Varianzen und Standardabweichungen berechnen.
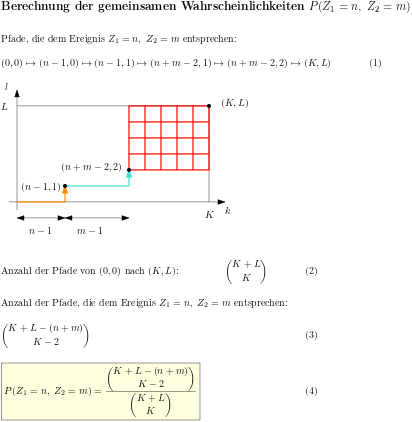
Die hypergeometrische Verteilung beschreibt die Wahrscheinlichkeit dafür, dass beim Ziehen ohne Zurücklegen n Treffer aus einer Urne gezogen werden; dazu befinden sich in der Urne anfangs L Treffer und K Nieten und es werden N Lose entnommen. Die Abhängigkeit der Verteilung von den drei Parametern K, L und N erschwert den Zugang zur Berechnung der gesuchten Wahrscheinlichkeiten. Es werden zwei - natürlich gleichwertige - Methoden gezeigt, wie man die Wahrscheinlichkeiten berechnet.
Das Abzählproblem "Ziehen ohne Zurücklegen" wird unter der Annahme betrachtet, dass sich in der Urne zwei Arten von Objekten befinden (etwa K Nieten und L Treffer). Berechnet wird die Anzahl der möglichen Ergebnisse, wenn N-mal ein Los aus der Urne gezogen wird und dabei die Reihenfolge der Ergebnisse beachtet wird.
Ebenso wird gezeigt, wie man die möglichen Ergebnisse mit Hilfe des Hamming-Abstandes charakterisieren und mit Hilfe des N-dimensionalen Hyperwürfels und im Pascalschen Dreieck veranschaulichen kann. In den R-Skripten werden Algorithmen für das Abzählproblem und die Berechnung der möglichen Ergebnisse vorgestellt und diskutiert.
Die Funktion sample() wird verwendet, um Stichproben zu erzeugen. Damit dies nicht zu unerwünschtem Verhalten führt, muss man wissen, dass der Aufruf an sample.int() weitergereicht wird, wenn die Menge, aus der ein Objekt ausgewählt werden soll, nur ein Element besitzt. Es wird ein Beispiel ausführlich besprochen, bei dem eine naheliegende Implementierung zu unerwarteten Ergebnissen führt.
Die Funktion sample() wird verwendet, um Stichproben zu erzeugen. Sie lässt sich so konfigurieren, dass man die Wahrscheinlichkeitsverteilungen von beliebigen selbstdefinierten diskreten Zufallsvariablen einsetzen kann. Zudem kann man das Ziehen mit beziehungsweise ohne Zurücklegen realisieren.