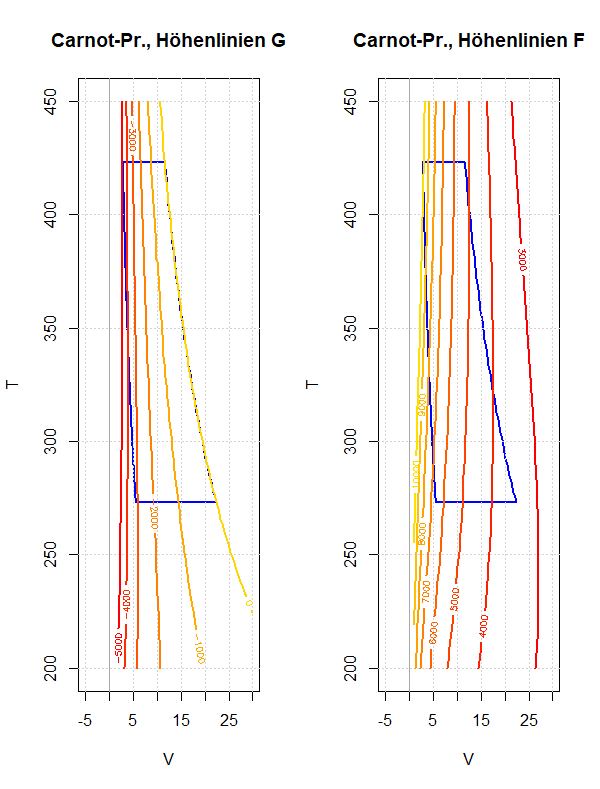
Die freie Energie und die gebundene Energie beim Carnot-Prozess
Am Beispiel des Carnot-Prozesses soll das Verhalten der freien und der gebundenen Energie während eines Umlaufs diskutiert werden. Dies soll die Bedeutung dieser thermodynamischen Potentiale besser verständlich machen; speziell ob und wie sie als Arbeitsfähigkeit beziehungsweise Wärmeinhalt eines Systems interpretiert werden können.